Difference between revisions of "Coupled Traction Law"
| Line 13: | Line 13: | ||
where T<sub>n</sub> and T<sub>t</sub> are the normal and tangential tractions and δ<sub>n</sub> and δ<sub>t</sub> are the normal and tangential CODs. | where T<sub>n</sub> and T<sub>t</sub> are the normal and tangential tractions and δ<sub>n</sub> and δ<sub>t</sub> are the normal and tangential CODs. | ||
This law can be expressed using damage mechanics by defining an effective slope of | |||
| |||
<math>k_{eff}=(1-D)k</math> | |||
where k is the initial slope of the curve and D is a damage parameter. This effective slope describes a line from the origin to the point on the triangular curve corresponding to the maximum displacement seen on the current particle. The effective traction along that line is | |||
| |||
<math>T_{eff}=k_{eff}\delta_{eff}</math> | |||
The effective stiffness is found using | |||
| |||
<math>(1-D)={\delta_{pk}(\delta_c-\delta_{max})\over\delta_{max}(\delta_c-\delta_{pk})</math> | |||
where <code>δ<sub>c</sub></code> is the critical effective cod and <code>δ<sub>max</sub></code> is the maximum effective cod seen on the crack particle, except that it is initialized to the peak cod (δ<sub>pk</sub>) at the start of the calculations. By this relation, D = 0 until the effective cod passes the peak cod. Thereafter, D increases from 0 at the peak to 1 at the critical cod. Once D is found, the normal and tangential tractions are <code>T<sub>n</sub> = k<sub>eff</sub>δ<sub>n</sub></code> and <code>T<sub>t</sub> = k<sub>eff</sub>δ<sub>t</sub></code>, which satisfy the effective traction - effective cod law given above. Note that during monotonic loading the traction will remain on the curve. If unloading occurs, however, the tractions follow a line back to the original from the maximum cod. | |||
== Failure == | == Failure == | ||
| Line 18: | Line 35: | ||
== Traction Law Properties == | == Traction Law Properties == | ||
The | The use of effective terms is meant to account for mixed mode effects in a single coupled traction law. The properties you enter are the same as defined in the Triangular Traction Law and they all mean the same thing for this traction law, except they apply now to effective traction and critical effective cod rather than mode I traction and critical cod. JIc is the total energy release rate from area on the effective traction - effective cod curve. The mode II properties are ignored. | ||
{| class="wikitable" | {| class="wikitable" | ||
Revision as of 18:44, 7 January 2014
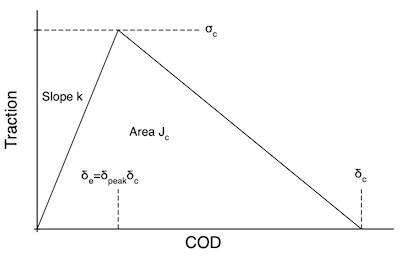
The Traction Law
This traction law is the same as the triangular traction law except that COD and traction are now effective terms that are related to normal and tangential components of traction and displacement:
[math]\displaystyle{ {\rm Traction} = T_{eff} \qquad{\rm where} \qquad T_{eff} = \sqrt{T_n^2+T_t^2} }[/math]
[math]\displaystyle{ {\rm cod} = \delta_{eff} \qquad{\rm where} \qquad \delta_{eff} = \sqrt{\delta_n^2+\delta_t^2} }[/math]
where Tn and Tt are the normal and tangential tractions and δn and δt are the normal and tangential CODs.
This law can be expressed using damage mechanics by defining an effective slope of
[math]\displaystyle{ k_{eff}=(1-D)k }[/math]
where k is the initial slope of the curve and D is a damage parameter. This effective slope describes a line from the origin to the point on the triangular curve corresponding to the maximum displacement seen on the current particle. The effective traction along that line is
[math]\displaystyle{ T_{eff}=k_{eff}\delta_{eff} }[/math]
The effective stiffness is found using
[math]\displaystyle{ (1-D)={\delta_{pk}(\delta_c-\delta_{max})\over\delta_{max}(\delta_c-\delta_{pk}) }[/math]
where δc is the critical effective cod and δmax is the maximum effective cod seen on the crack particle, except that it is initialized to the peak cod (δpk) at the start of the calculations. By this relation, D = 0 until the effective cod passes the peak cod. Thereafter, D increases from 0 at the peak to 1 at the critical cod. Once D is found, the normal and tangential tractions are Tn = keffδn and Tt = keffδt, which satisfy the effective traction - effective cod law given above. Note that during monotonic loading the traction will remain on the curve. If unloading occurs, however, the tractions follow a line back to the original from the maximum cod.
Failure
Traction Law Properties
The use of effective terms is meant to account for mixed mode effects in a single coupled traction law. The properties you enter are the same as defined in the Triangular Traction Law and they all mean the same thing for this traction law, except they apply now to effective traction and critical effective cod rather than mode I traction and critical cod. JIc is the total energy release rate from area on the effective traction - effective cod curve. The mode II properties are ignored.
| Property | Description | Units | Default |
|---|---|---|---|
| (other) | Properties common to all traction laws | varies | varies |