Difference between revisions of "First Order Phase Transition Material"
| (40 intermediate revisions by 2 users not shown) | |||
| Line 24: | Line 24: | ||
=== Modeling with a Finite Width Transition === | === Modeling with a Finite Width Transition === | ||
One approach to modeling a first order transition is to spread out the transition region and allow ΔC and Δα to depend on temperature within that region. We can define ''f<sub>L</sub>'' as the fraction of the material that is liquid where ''f<sub>L</sub>'' transitions from 0 in | One approach to modeling a first order transition is to spread out the transition region and allow ΔC and Δα to depend on temperature within that region. We can define ''f<sub>L</sub>'' as the fraction of the material that is liquid where ''f<sub>L</sub>'' transitions from 0 at T<sub>m</sub>-ΔT (in solid phase) to 1 at T<sub>m</sub>+ΔT (in liquid phase) where ΔT is finite transition width selected for the transition. The excess heat capacity and thermal expansion within the transition region can then be written as: | ||
| | ||
| Line 30: | Line 30: | ||
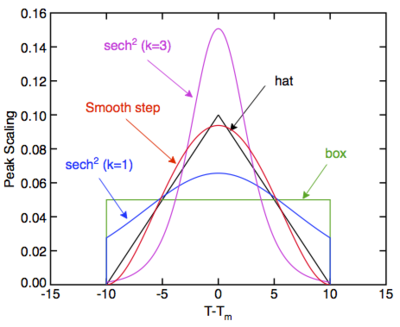
This material can use several different ''f<sub>L</sub>'' functions: | This material can use several different ''f<sub>L</sub>'' functions: | ||
[[File:TransitionPeaks.png|400px|right]] | |||
<ul> | <ul> | ||
<li>Hat (shape 0): This option uses a piece-wise quadratic function for ''f<sub>L</sub>'' such that | <li>Hat (shape 0): This option uses a piece-wise quadratic function for ''f<sub>L</sub>'' such that transition peak is triangular "hat" function with peak ΔC of ΔH<sub>f</sub>/ΔT and peak Δα of ΔV<sub>f</sub>/ΔT at T<sub>m</sub>.</li> | ||
<li>Box (shape 1): This option sets ''f<sub>L</sub>'' to a linear function | <li>Box (shape 1): This option sets ''f<sub>L</sub>'' to a linear function from 0 to 1 that results in constant ΔC = ΔH<sub>f</sub>/(2ΔT) and Δα = ΔV<sub>f</sub>/(2ΔT) within the transition.</li> | ||
<li> | <li>sech<sup>2</sup> (shape 2): This option sets ''f<sub>L</sub>'' to a truncated and normalized exponential step function: | ||
<br><br> | <br><br> | ||
| | ||
<math>f_L = \frac{1}{2}\left[1-\tanh\left(\frac{T-T_m}{\Delta T}\right)\right]</math> | <math>f_L = \frac{1}{2}\left[1-\coth(k)\tanh\left(\frac{k(T-T_m)}{\Delta T}\right)\right]</math> | ||
<br><br>The resulting | <br><br>The resulting peak follows a sech<sup>2</sup> function with peak ΔC of k coth(k)ΔH<sub>f</sub>/(2ΔT) and Δα of k coth(k)ΔV<sub>f</sub>/(2ΔT) at T<sub>m</sub>. Here k is a parameter characterizing sharpness of the transition. As k approaches zero, this shape become a box shape. As k increases the peak gets sharper and approaches Dirac δ(T-T<sub>m</sub>) function for large k. Choosing very high k effectively makes the transition very stiff and simulations lose accuracy unless transitions occur very slowly. The default value is k = 3. | ||
</li> | </li> | ||
<li>Smooth Step (shape 3): This option sets ''f<sub>L</sub>'' to | <li>Smooth Step (shape 3): This option sets ''f<sub>L</sub>'' to a [https://en.wikipedia.org/wiki/Smoothstep fifth-order step function] from 0 to 1 such that peak shape has zero slopes at T<sub>melt</sub>-ΔT and T<sub>melt</sub>+ΔT and peak ΔC of 15ΔH<sub>f</sub>/(16ΔT) and peak Δα of 15ΔV<sub>f</sub>/(16ΔT) at T<sub>m</sub> | ||
</ul> | </ul> | ||
The | The figure on the right plots the above shapes for ΔT = 10 degrees. | ||
[[ | For numerical modeling, you enter the total heat of fusion, ''f<sub>L</sub>'' shape style, transition width parameter ΔT, and peak shape factor (if needed, such as k for shape=2). The same transition function is used for Δα where ΔV<sub>f</sub> is found from density difference between solid and liquid phases. Because implementation of heat of fusion is done through heat capacity, all simulations with phase transition materials should activate [[Thermal_Calculations#Conduction|coupled conduction calculations]] (conduction is also needed to see changes in temperature that can lead to phase changes). The values for ΔT and peak shape function may need to varied for numerical stability in specific problems. | ||
=== Modeling with a Sharp Transition === | |||
If the ΔT is set to zero, the phase transition will be modeled but will hold the particle temperature at T<sub>melt</sub> until enough heat has transferred into (or out of) the material to melt (or solidify) the material. | |||
=== Transition Temperature Range === | === Transition Temperature Range === | ||
| Line 57: | Line 61: | ||
== Material Properties == | == Material Properties == | ||
The | The material properties are entered using: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 71: | Line 75: | ||
| Tsigma || The standard deviation for the transition temperature (K). The temperature range will be limited to +/- three standard deviations || K || 0 | | Tsigma || The standard deviation for the transition temperature (K). The temperature range will be limited to +/- three standard deviations || K || 0 | ||
|- | |- | ||
| DeltaT || A | | DeltaT || A transition width for application of increased heat capacity and increased thermal expansion. If ΔT<=0, the transition is sharp at the melting point. || K || 10 | ||
|- | |||
| PeakShape || Peak style for transition region: 0=hat, 1=box, 2=sech<sup>2</sup>, 3=smooth step as described above || none || 3 | |||
|- | |||
| PeakArg || Peak argument (only used for sech<sup>2</sup> as k parameter) || none || 3 | |||
|- | |- | ||
| Hfusion || The heat of fusion for the transition || [[ConsistentUnits Command#Legacy and Consistent Units|heat of fusion units]] || 0 | | Hfusion || The heat of fusion for the transition || [[ConsistentUnits Command#Legacy and Consistent Units|heat of fusion units]] || 0 | ||
| Line 80: | Line 88: | ||
== History Variables == | == History Variables == | ||
This material tracks two history variables: | This material tracks two history variables if ΔT>0 and three if ΔT<=0 (''i.e.'', when using a sharp transition): | ||
# The currently active phase with 0 for solid phase and 1 for liquid phase. | # The currently active phase with 0 for solid phase and 1 for liquid phase. When modeling a sharp transition, this value will range form 0 to 1 to indicate fraction liquid state. | ||
# The melting point of the particle. It is constant throughout the analysis, but can be visualized as random variable if Tsigma>0. | # The melting point of the particle. It is constant throughout the analysis, but can be visualized as random variable if Tsigma>0. | ||
# Particle ΔV in time step during transition when modeled with a sharp transition (only when ΔT<=0). | |||
History variables greater than ''n'' (where ''n''=2 for ΔT>0 and ''n''=3 for ΔT<=0) will be for the solid or the liquid material. If the solid material as ''s'' history variable and liquid has ''l'' variables, the variables are access by number using | |||
# Solid variables 1 to ''s'' are in history ''n''+1 to ''n+s'' | |||
# Liquid variables 1 to ''l'' are in history variables ''n+s''+1 to ''n+s+l'' | |||
== Examples == | == Examples == | ||
Material "solid","Neohookean Material","Neohookean" | |||
E 10 | |||
nu .33 | |||
rho 1 | |||
alpha 40 | |||
kCond 200 | |||
Cv 21.13 | |||
Done | |||
Material "liquid","Liquid Material","TaitLiquid" | |||
K 2.5 | |||
viscosity 50 | |||
rho 1 | |||
kCond 100 | |||
Cv 41.13 | |||
alpha 70 | |||
Done | |||
Material "phases","Transition Material","PhaseTransition" | |||
SolidPhase "solid" | |||
LiquidPhase "liquid" | |||
Tmelt 310 | |||
DeltaT 5 | |||
Tsigma 3 | |||
Hfusion 250 | |||
Done | |||
Latest revision as of 14:31, 26 June 2019
First Order Phase Transition
This exploratory MPM material models a first order phase transition between two materials (it is currently only available in OSParticulas). It has no material response itself. Instead, it acts as a "parent" material to two "child" materials, where one child is a "solid phase" and the other is a "liquid" phase. The properties of this material control transition from the solid to liquid phase, where solid is the low-temperature phase, and the liquid is the high temperature phase.
A first order phase transition occurs at a melting temperature, Tmelt. The meaning of a first order transition is that thermodynamic energy functions (e.g., Gibbs free energy) are continuous at Tmelt, but the phase which is the lowest energy changes. Although free energy is constant, the first derivatives of free energy undergo a discrete change (hence the origin of the term first-order transition). Namely, there is a change in enthalpy (ΔHf), entropy (ΔSf), and volume (ΔVf), where subscript "f" means fusion. Because free energies of the two phases are equal at Tmelt, the first two are related by
[math]\displaystyle{ \Delta G(T_m) = 0 = \Delta H_f - T_m \Delta S_f \qquad{\rm or}\qquad \Delta S_f = {\Delta H_f\over T_m} }[/math]
Enthalpy and Volume Changes in the Transition
Most materials do not have a sharp transition, but rather undergo a transition over a range of temperatures, such as from Ti to Tf. The enthalpy of fusion is experimentally related to the heat capacity during this transition by:
[math]\displaystyle{ \Delta H_f = \int_{T_i}^{T_f} \Delta C\ dT }[/math]
where ΔC is the excess heat capacity during the transition compared to the heat capacity of the material in the absence of a transition. Likewise, the density of the liquid will differ from the density of the solid, which means there is a volume change of fusion. The volume change of fusion can be expressed from thermal expansion (or shrinkage) during the transition of
[math]\displaystyle{ \Delta V_f = \int_{T_i}^{T_f} \Delta \alpha\ dT }[/math]
where Δα is the excess thermal expansion during the transition compared to the thermal expansion of the material in the absence of a transition.
Modeling with a Finite Width Transition
One approach to modeling a first order transition is to spread out the transition region and allow ΔC and Δα to depend on temperature within that region. We can define fL as the fraction of the material that is liquid where fL transitions from 0 at Tm-ΔT (in solid phase) to 1 at Tm+ΔT (in liquid phase) where ΔT is finite transition width selected for the transition. The excess heat capacity and thermal expansion within the transition region can then be written as:
[math]\displaystyle{ \Delta C = \Delta H_f \frac{df_L}{dT} \qquad{\rm and}\qquad \Delta \alpha = \Delta V_f \frac{df_L}{dT} }[/math]
This material can use several different fL functions:
- Hat (shape 0): This option uses a piece-wise quadratic function for fL such that transition peak is triangular "hat" function with peak ΔC of ΔHf/ΔT and peak Δα of ΔVf/ΔT at Tm.
- Box (shape 1): This option sets fL to a linear function from 0 to 1 that results in constant ΔC = ΔHf/(2ΔT) and Δα = ΔVf/(2ΔT) within the transition.
- sech2 (shape 2): This option sets fL to a truncated and normalized exponential step function:
[math]\displaystyle{ f_L = \frac{1}{2}\left[1-\coth(k)\tanh\left(\frac{k(T-T_m)}{\Delta T}\right)\right] }[/math]
The resulting peak follows a sech2 function with peak ΔC of k coth(k)ΔHf/(2ΔT) and Δα of k coth(k)ΔVf/(2ΔT) at Tm. Here k is a parameter characterizing sharpness of the transition. As k approaches zero, this shape become a box shape. As k increases the peak gets sharper and approaches Dirac δ(T-Tm) function for large k. Choosing very high k effectively makes the transition very stiff and simulations lose accuracy unless transitions occur very slowly. The default value is k = 3. - Smooth Step (shape 3): This option sets fL to a fifth-order step function from 0 to 1 such that peak shape has zero slopes at Tmelt-ΔT and Tmelt+ΔT and peak ΔC of 15ΔHf/(16ΔT) and peak Δα of 15ΔVf/(16ΔT) at Tm
The figure on the right plots the above shapes for ΔT = 10 degrees.
For numerical modeling, you enter the total heat of fusion, fL shape style, transition width parameter ΔT, and peak shape factor (if needed, such as k for shape=2). The same transition function is used for Δα where ΔVf is found from density difference between solid and liquid phases. Because implementation of heat of fusion is done through heat capacity, all simulations with phase transition materials should activate coupled conduction calculations (conduction is also needed to see changes in temperature that can lead to phase changes). The values for ΔT and peak shape function may need to varied for numerical stability in specific problems.
Modeling with a Sharp Transition
If the ΔT is set to zero, the phase transition will be modeled but will hold the particle temperature at Tmelt until enough heat has transferred into (or out of) the material to melt (or solidify) the material.
Transition Temperature Range
The temperature range for which a material undergoes a transition is commonly caused by spatial heterogeneity in the object. For example, polymer materials (which have a particularly large temperature range for first order transitions) have wide variation in crystal perfection and therefore a wide temperature range for melting. The ΔT property mentioned above is one way to model a temperature range, but that parameter is more associated with numerical implementation of implementing an infinite heat capacity or infinite thermal expansion that is seen for a sharp transitions. A second approach to modeling a transition temperature range is to allow Tmelt to be a random variable representing heterogeneity in the crystal structures. This form of variation is modeled by entering the standard deviation for the melting temperature. It can be picked based on observations of the width of the melting transition.
The current implementation randomly assigns a normal distribution of melting points to all particles with zero spatial correlation. In the future, spatial correlation will be added.
Material Properties
The material properties are entered using:
| Property | Description | Units | Default |
|---|---|---|---|
| SolidPhase | Enter the solid phase material by ID (scripted files only) or by number | none | none |
| LiquidPhase | Enter the liquid phase material by ID (scripted files only) or by number | none | none |
| Tmelt | The transition temperature (K). The solid phase is stable below Tmelt and liquid phase above it | K | none |
| Tsigma | The standard deviation for the transition temperature (K). The temperature range will be limited to +/- three standard deviations | K | 0 |
| DeltaT | A transition width for application of increased heat capacity and increased thermal expansion. If ΔT<=0, the transition is sharp at the melting point. | K | 10 |
| PeakShape | Peak style for transition region: 0=hat, 1=box, 2=sech2, 3=smooth step as described above | none | 3 |
| PeakArg | Peak argument (only used for sech2 as k parameter) | none | 3 |
| Hfusion | The heat of fusion for the transition | heat of fusion units | 0 |
Note that the materials that are capable of being phase materials are limited to those that have been revised to work with this phase transition material. The currently allowed materials are Mooney Material, Neo-Hookean Material, Isotropic, Hyperelastic-Plastic Material, Isotropic, Hyperelastic-Plastic Mie-Grüneisen Material, Clamped Neo-Hookean Material, and Tait Liquid Material.
History Variables
This material tracks two history variables if ΔT>0 and three if ΔT<=0 (i.e., when using a sharp transition):
- The currently active phase with 0 for solid phase and 1 for liquid phase. When modeling a sharp transition, this value will range form 0 to 1 to indicate fraction liquid state.
- The melting point of the particle. It is constant throughout the analysis, but can be visualized as random variable if Tsigma>0.
- Particle ΔV in time step during transition when modeled with a sharp transition (only when ΔT<=0).
History variables greater than n (where n=2 for ΔT>0 and n=3 for ΔT<=0) will be for the solid or the liquid material. If the solid material as s history variable and liquid has l variables, the variables are access by number using
- Solid variables 1 to s are in history n+1 to n+s
- Liquid variables 1 to l are in history variables n+s+1 to n+s+l
Examples
Material "solid","Neohookean Material","Neohookean" E 10 nu .33 rho 1 alpha 40 kCond 200 Cv 21.13 Done Material "liquid","Liquid Material","TaitLiquid" K 2.5 viscosity 50 rho 1 kCond 100 Cv 41.13 alpha 70 Done Material "phases","Transition Material","PhaseTransition" SolidPhase "solid" LiquidPhase "liquid" Tmelt 310 DeltaT 5 Tsigma 3 Hfusion 250 Done