Triangular Traction Law

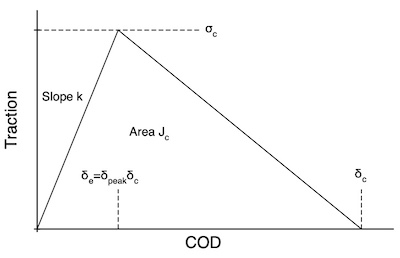
The Traction Law

This traction law assumes the triangular shape for the cohesive law as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II).

The toughness of this cohesive law is the area under the curve or:

      [math]\displaystyle{ J_c = {1\over 2} \sigma_c\delta_c }[/math]

When creating this traction law, you have to enter exactly two of these three properties for both mode I and mode II (i.e., two of J_Ic, σ_I, and δ_Ic and two of J_IIc, σ_II, and δ_IIc). Whichever property is not specified will be calculated from the two provided properties using one of the following relations:

      [math]\displaystyle{ \delta_c = {2J_c\over \sigma_c}, \qquad \sigma_c = {2J_c\over \delta_c}, \qquad {\rm or} \qquad J_c = {1\over 2}\sigma_c\delta_c }[/math]

The initial linear-elastic rise can be defined by slope k or by the relative crack opening displacement at the peak stress, δ_peak (which is entered relative to the critical opening displacement or the elastic COD to reach the peak is δ_e = δ_peakδ_c). You can only enter one of these two properties (i.e., one of k_Ie and δ_I,peak and one of k_IIe and δ_II,peak). The other will be calculated from:

      [math]\displaystyle{ k = {\sigma_c\over \delta_{peak}\delta_c} \qquad {\rm or} \qquad \delta_{peak} = {\sigma_c\over k\delta_c} }[/math]

Alternatively, you can omit both k and δ_peak. In the case, the default peak will be located at δ_peak = 0.225926299. This location provides the closest match to the cubic traction law for area under the curve as a function of COD. The initial slope will be set to

      [math]\displaystyle{ k = {\sigma_c\over 0.225926299 \delta_c} }[/math]

This implementation disallows zero of infinite initial stiffness (for stability reasons). In other words, the entered parameters must resolve to k>0 and δ_peak>0.

Failure

The entered traction laws give mode I or mode II cohesive laws for pure mode I or pure mode II loading. Under pure mode load, the cohesive law will fail (and release the crack surfaces) when the COD reaches the critical COD ()δ_c for that mode.

For mixed-mode loading, the normal and and shear tractions still depend only on normal and shear displacements, respectively, but the conditions for failure change. For mixed-mode loading, failure occurs when:

      [math]\displaystyle{ \left({G_I\over J_{Ic}}\right)^{n} + \left({G_{II}\over J_{IIc}}\right)^{n} = 1 }[/math]

where G_I and G_II are areas under mode I and mode II traction laws up to current maximum COD and n is mixed-mode failure criterion parameter. This failure criterion will mean that failure may occur when normal or shear tractions are nonzero. In other words, each traction law will have COD less then their critical COD, which means their traction will be greater than zero. Because failure released the crack surface, mixed-mode failure by this criterion may result in a sudden drop of finite normal and shear traction to zero traction. This approach is identical to the one adopted by Thouless et. al to handle mixed-mode loading and appears to work well.

Some models have coupled the mode I and II traction laws such that they always approach zero at time of failure (e.g., work of Högberg (2006), Camacho and Ortiz (1996), and Comanho (1996)). The Högberg model is implemented in the Coupled Triangular Traction Law. But these approaches are based on defining an effective displacement. A recent re-analysis of cohesive zones has shown these models are invalid unless the normal and tangential laws are scaled copies of each other. A better approach based on this work that couples mode I and mode II and remains valid for arbitrary normal and tangential laws is now the recommended model for mixed-mode failure simulations.

Traction Law Properties

The following properties are used to create a triangular traction law:

Property	Description	Units	Default
kIe	Initial elastic slope when opened, k in mode I	pressure/length units	none
delpkI	COD for peak stress, δpeak, relative to critical COD in mode I (0 to 1)	dimensionless	none
kIIe	Initial elastic slope, k in mode II	pressurelength units	none
delpkII	COD for peak stress, δpeak, relative to critical COD in mode II (0 to 1)	dimensionless	none
(other)	Properties common to all traction laws	varies	varies

The resulting laws are required to have kIe, delpkI, kIIe, and delpkII as entered (or as calculated) must all be greater than zero. In other words, for stability reasons, the initial stiffness cannot be infinite.