Difference between revisions of "Exponential Traction Law"
| Line 2: | Line 2: | ||
== The Traction Law == | == The Traction Law == | ||
[[File: | [[File:Exptraction.jpg|right]] | ||
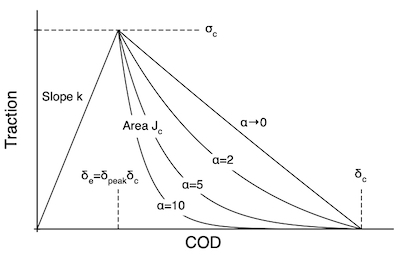
This [[Traction Laws|traction law]] assumes a linear elastic response up to σ<sub>c</sub> followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δ<sub>c</sub>. The exponential decay in the post peak region (''i.e.'', δ>δ<sub>e</sub>) is given by | This [[Traction Laws|traction law]] assumes a linear elastic response up to σ<sub>c</sub> followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δ<sub>c</sub>. The exponential decay in the post peak region (''i.e.'', δ>δ<sub>e</sub>) is given by | ||
| Line 11: | Line 11: | ||
This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II). | This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II). | ||
The toughness of this cohesive law is the area under the curve | Notice how the shape changes with α. In the limit of α=0, this law is identical to the [[Triangular Traction Law]] (and that one should be used instead because it is more efficient. Increasing α causes traction to drop faster, which might model transition to a more brittle material. The toughness of this cohesive law is the area under the curve that can be case aas | ||
| | ||
<math>J_c = {1\over 2} \sigma_c\delta_c</math> | <math>J_c = {1\over 2} \sigma_c\delta_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right) | ||
\quad{\rm where}\quad f(\alpha) = 2\left(\frac{1}{\alpha}-\frac{e^{-\alpha}}{1-e^{-\alpha}}\right)</math> | |||
When creating this traction law, you have to enter <i>exactly</i> two of these three properties for both mode I and mode II ''(i.e.'', two of J<sub>Ic</sub>, σ<sub>I</sub>, and δ<sub>Ic</sub> and two of J<sub>IIc</sub>, σ<sub>II</sub>, and δ<sub>IIc</sub>). Whichever property is not specified will be calculated from the two provided properties using one of the following relations: | When creating this traction law, you have to enter <i>exactly</i> two of these three properties for both mode I and mode II ''(i.e.'', two of J<sub>Ic</sub>, σ<sub>I</sub>, and δ<sub>Ic</sub> and two of J<sub>IIc</sub>, σ<sub>II</sub>, and δ<sub>IIc</sub>). Whichever property is not specified will be calculated from the two provided properties using one of the following relations: | ||
Revision as of 14:21, 21 December 2020
The Traction Law
This traction law assumes a linear elastic response up to σc followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δc. The exponential decay in the post peak region (i.e., δ>δe) is given by
[math]\displaystyle{ S(\delta) = \sigma_c\frac{e^{-\alpha\frac{\delta-\delta_e}{\delta_c-\delta_e}}-e^{-\alpha}}{1-e^{-\alpha}} }[/math]
This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II).
Notice how the shape changes with α. In the limit of α=0, this law is identical to the Triangular Traction Law (and that one should be used instead because it is more efficient. Increasing α causes traction to drop faster, which might model transition to a more brittle material. The toughness of this cohesive law is the area under the curve that can be case aas
[math]\displaystyle{ J_c = {1\over 2} \sigma_c\delta_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right) \quad{\rm where}\quad f(\alpha) = 2\left(\frac{1}{\alpha}-\frac{e^{-\alpha}}{1-e^{-\alpha}}\right) }[/math]
When creating this traction law, you have to enter exactly two of these three properties for both mode I and mode II (i.e., two of JIc, σI, and δIc and two of JIIc, σII, and δIIc). Whichever property is not specified will be calculated from the two provided properties using one of the following relations:
[math]\displaystyle{ \delta_c = {2J_c\over \sigma_c}, \qquad \sigma_c = {2J_c\over \delta_c}, \qquad {\rm or} \qquad J_c = {1\over 2}\sigma_c\delta_c }[/math]
The initial linear-elastic rise can be defined by slope k or by the relative crack opening displacement at the peak stress, δpeak (which is entered relative to the critical opening displacement or the elastic COD to reach the peak is δe = δpeakδc). You can only enter one of these two properties (i.e., one of kIe and δI,peak and one of kIIe and δII,peak). The other will be calculated from: This traction law assumes the triangular shape for traction as a function of crack opending displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled traction laws for opening displacement (mode I) and sliding displacement (mode II).
The toughness of this traction law is the area under the curve or:
[math]\displaystyle{ J_c = {1\over 2} \sigma\delta_c }[/math]
When creating this traction law, you have to enter exactly two of these three properties for both mode I and mode II (i.e., two of JIc, σI, and δIc and two of JIIc, σII, and δIIc). Whichever property is not specified will be calculated from the two provided properties using one of the following relations:
[math]\displaystyle{ \delta_c = {2J_c\over \sigma}, \qquad \sigma = {2J_c\over \delta_c}, \qquad {\rm or} \qquad J_c = {1\over 2}\sigma\delta_c }[/math]