Difference between revisions of "Coupled Traction Law"
| Line 36: | Line 36: | ||
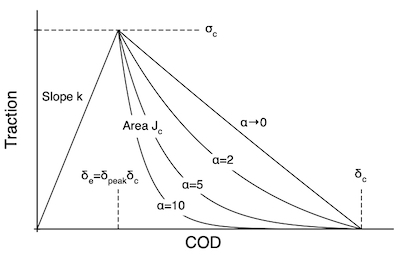
See figure above for effect of α on the decay rate (note that α=0 is identical to linear decay). | See figure above for effect of α on the decay rate (note that α=0 is identical to linear decay). | ||
== Failure == | |||
Under pure mode I or pure mode II, a coupled traction law and its failure are identical to a [[Triangular Traction Law|triangular cohesive law]] or an [[Exponential Traction Law|exponential cohesive law]]. Under mixed-mode conditions, however, these laws differ. [[Triangular Traction Law|Triangular]] and [[Exponential Traction Law|exponential]] cohesive law have to impose a [[Triangular Traction Law#Failure|mixed-mode failure criterion]]. This model does not need such a criterion. It fails naturally when λ reaches one. Despite this advantage of failing "naturally", the Högberg model <ref name="hogberg"/> has limitations explained in the next section. | |||
== Property Limitations == | == Property Limitations == | ||
| Line 47: | Line 51: | ||
Note that this implementation lets you choose properties that make the modeling invalid. That option is allowed for comparison of the published model to other models. If you do select invalid properties, the output file will include a warning. The preferred model for simulations of mixed-mode failure is the [[Mixed Mode Traction Law]]. | Note that this implementation lets you choose properties that make the modeling invalid. That option is allowed for comparison of the published model to other models. If you do select invalid properties, the output file will include a warning. The preferred model for simulations of mixed-mode failure is the [[Mixed Mode Traction Law]]. | ||
== Alternate Effective Displacement Method == | == Alternate Effective Displacement Method == | ||
Revision as of 11:38, 29 December 2020
The Traction Law
(This documentation is implementation of this law OSParticulas that is coming soon to NairnMPM. The current implementation in NairnMPM is different and should not be used until updated to this new implementation).
This traction law uses either the triangular cohesive law or the exponential cohesive law but couples the normal and tangential displacements by using an effective displacement. This implementation follows methods derived in a paper by Högberg [1]. The Högberg effective displacement is defined by
[math]\displaystyle{ \lambda = \sqrt{\left(\frac{u_n}{\delta_c^{(n)}}\right)^2 +\left(\frac{u_t}{\delta_c^{(t)}}\right)^2} }[/math]
where u is displacement, δc is displacement at failure (see figure), and "n" and "t" refer to normal an tangential directions. In terms of λ, the normal an tangential tractions are:
[math]\displaystyle{ \left(T^{(n)},T^{(t)}\right) = \frac{H(\lambda_\omega)}{\lambda_\omega} \left(\frac{\sigma_{c}^{(n)} u_n}{\delta_c^{(n)}},\frac{\sigma_{c}^{(t)} u_t}{\delta_c^{(t)}}\right) }[/math]
where λ\omega; is a damage parameter equal to the maximum value of λ during a simulation. These traction apply after initiation that occurs when λ reaches λp(θ) defined by
[math]\displaystyle{ \frac{1}{ \lambda_p(\theta)} = \sqrt{\left(\frac{\delta_c^{(n)}\sin\theta}{\delta_e^{(n)}}\right)^2 + \left(\frac{\delta_c^{(t)}\cos\theta}{\delta_e^{(t)}}\right)^2} \quad {\rm with} \quad \theta = \frac{\delta_c^{(t)}u_n}{\delta_c^{(n)}u_t} }[/math]
and δe is displacement at end of the elastic regime. Finally, Högberg assumed H(λ) is defined by linear decay from 1 when λ=λp(θ) to zero when λ=1:
[math]\displaystyle{ H(\lambda) = \frac{1-\lambda}{1-\lambda_p(\theta)} }[/math]
This implementation has extended the Höberg approach to also allow an exponential decay using:
[math]\displaystyle{ H(\lambda) = \frac{e^{-\alpha\frac{\lambda-\lambda_p(\theta)}{1-\lambda_p(\theta)}}-e^{-\alpha}}{1-e^{-\alpha}} }[/math]
See figure above for effect of α on the decay rate (note that α=0 is identical to linear decay).
Failure
Under pure mode I or pure mode II, a coupled traction law and its failure are identical to a triangular cohesive law or an exponential cohesive law. Under mixed-mode conditions, however, these laws differ. Triangular and exponential cohesive law have to impose a mixed-mode failure criterion. This model does not need such a criterion. It fails naturally when λ reaches one. Despite this advantage of failing "naturally", the Högberg model [1] has limitations explained in the next section.
Property Limitations
The Höberg model [1] seemingly depends on independent normal and traction law properties that could be entered as for triangular or the exponential cohesive laws. In fact Ref. [1] claims independent properties are allowed. A new analysis of cohesive zone modeling [2] has revealed, however, that the Högberg model is always invalid for mixed mode loading unless properties are chosen such that
[math]\displaystyle{ \frac{\delta_e^{(n)}}{\delta_c^{(n)}} = \frac{\delta_e^{(t)}}{\delta_c^{(t)}} }[/math]
In other words, the ratio of displacement at peak stress to displacment and failure must be the same for both normal and tangential directions. When use the exponential extension of the Högberg model the α coefficent must also be the same for normal and tangential directions.
Note that this implementation lets you choose properties that make the modeling invalid. That option is allowed for comparison of the published model to other models. If you do select invalid properties, the output file will include a warning. The preferred model for simulations of mixed-mode failure is the Mixed Mode Traction Law.
Alternate Effective Displacement Method
except that COD and traction are now effective terms that are related to normal and tangential components of traction and displacement:
[math]\displaystyle{ {\rm Traction} = T_{eff} \qquad{\rm where} \qquad T_{eff} = \sqrt{T_n^2+T_t^2} }[/math]
[math]\displaystyle{ {\rm cod} = \delta_{eff} \qquad{\rm where} \qquad \delta_{eff} = \sqrt{\delta_n^2+\delta_t^2} }[/math]
where Tn and Tt are the normal and tangential tractions and δn and δt are the normal and tangential CODs.
This law can be expressed using damage mechanics by defining an effective slope of
[math]\displaystyle{ k_{eff}=(1-D)k }[/math]
where k is the initial slope of the curve and D is a damage parameter. This effective slope describes a line from the origin to the point on the triangular curve corresponding to the maximum displacement seen on the current particle. The effective traction along that line is
[math]\displaystyle{ T_{eff}=k_{eff}\delta_{eff} }[/math]
The effective stiffness is found using
[math]\displaystyle{ (1-D)={\delta_{pk}(\delta_c-\delta_{max})\over\delta_{max}(\delta_c-\delta_{pk})} }[/math]
where δc is the critical effective cod and δmax is the maximum effective cod seen on the crack particle, except that it is initialized to the peak cod (δpk) at the start of the calculations. By this relation, D = 0 until the effective cod passes the peak cod. Thereafter, D increases from 0 at the peak to 1 at the critical cod. Once D is found, the normal and tangential tractions are:
[math]\displaystyle{ T_n = k_{eff}\delta_n \qquad {\rm and} \qquad T_t = k_{eff}\delta_t }[/math]
Together, these traction satisfy the effective traction - effective cod law given above. Note that during monotonic loading the traction will remain on the curve. If unloading occurs, however, the tractions follow a line back to the original from the maximum cod.
Traction Law Properties
The properties you enter are the same as defined in
References
- ↑ 1.0 1.1 1.2 1.3 J. L. H ögberg, "Mixed mode cohesive law," International Journal of Fracture, 141, 549–559 (2006).
- ↑ J. A. Nairn and Y. E. Aimene "A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws" in preparation (2020).
- ↑ P. P. Camanho and C. G. Dàvila, "Mixed-mode decohesion finite elements for the simulation of delamination in composite materials," Technical Report, NASA/TM-2002-211737 (2002).
- ↑ G. T. Camacho and M. Ortiz, "Computational modelling of impact damage in brittle materials," Int. J. Solids Struct., 33, 2899–2938 (1996).