Difference between revisions of "Exponential Traction Law"
| (28 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== The Traction Law == | == The Traction Law == | ||
[[File: | [[File:Exptraction.jpg|right]] | ||
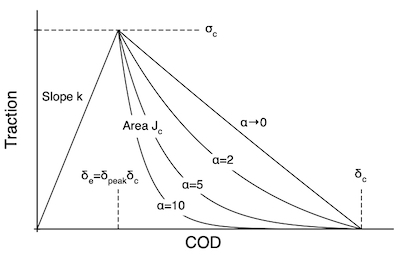
This [[Traction Laws|traction law]] assumes a linear elastic response up to σ<sub>c</sub> followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δ<sub>c</sub>. The exponential decay in the post peak region (''i.e.'', δ>δ<sub>e</sub>) is given by | This [[Traction Laws|traction law]] assumes a linear elastic response up to σ<sub>c</sub> followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δ<sub>c</sub>. The exponential decay in the post peak region (''i.e.'', δ>δ<sub>e</sub>) is given by | ||
| Line 11: | Line 11: | ||
This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II). | This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II). | ||
The toughness of this cohesive law is the area under the curve | Notice how the shape changes with α. In the limit of α=0, this law is identical to the [[Triangular Traction Law]] (and that one should be used instead because it is more efficient). Increasing α causes traction to drop faster, which might simulate increasingly brittle response. The toughness of this cohesive law is the area under the curve that can be cast as | ||
| | ||
<math>J_c = {1\over 2} \sigma_c\delta_c</math> | <math>J_c = {1\over 2} \sigma_c\delta_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right) | ||
\quad{\rm where}\quad f(\alpha) = 2\left(\frac{1}{\alpha}-\frac{e^{-\alpha}}{1-e^{-\alpha}}\right)</math> | |||
and δ<sub>peak</sub>=δ<sub>e</sub>/δ<sub>c</sub>. The function f(α) is 1 when α=0 and decays to zero as α increases. The toughness is thus bracketed by | |||
| | ||
<math> | <math>{1\over 2} \sigma_c\delta_e \le J_c \le {1\over 2} \sigma_c\delta_c</math> | ||
The | The minimum corresponds to large α with an instant drop to zero traction at δ<sub>e</sub> while the maximum corresponds to α=0 and is area under the corresponding [[Triangular Traction Law]]. | ||
When creating this traction law, you have to enter α, <i>exactly</i> two of σ<sub>c</sub>, δ<sub>peak</sub>, and k and <i>either</i> J<sub>c</sub> or δ<sub>c</sub>. These four required properties must be entered for both mode I and mode II. If you enter δ<sub>c</sub>, then the missing one of σ<sub>c</sub>, δ<sub>peak</sub>, and k is calculated from one of | |||
| | ||
<math> | <math>k = {\sigma_c\over \delta_{peak}\delta_c} \qquad {\rm or} \qquad \delta_{peak} = {\sigma_c\over k\delta_c} | ||
\qquad {\rm or} \qquad \sigma_c = k \delta_{peak}\delta_c | |||
</math> | |||
Finally J<sub>c</sub> is found from the expression above. If instead you enter J<sub>c</sub>, the calculation of δ<sub>c</sub> depends on which two of σ<sub>c</sub>, δ<sub>peak</sub>, and k are provided: | |||
| | ||
<math>\delta_c = {2J_c\ | <math>{\rm from\ }\sigma_c\ {\rm and}\ \delta_{peak}:\quad | ||
\delta_c = \frac{2J_c}{\sigma_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right)} | |||
</math> | |||
| |||
<math>{\rm from\ }\sigma_c\ {\rm and}\ k:\quad | |||
\delta_c = \frac{2kJ_c-\bigl(1-f(\alpha)\bigr)\sigma_c^2}{k\sigma_cf(\alpha)} | |||
</math> | |||
| |||
<math>{\rm from\ }\delta_{peak}\ {\rm and}\ k:\quad | |||
\delta_c = \sqrt{\frac{2J_c}{k\delta_{peak}\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right)}} | |||
</math> | |||
Once δ<sub>c</sub> is found, the remaining property among σ<sub>c</sub>, δ<sub>peak</sub>, and k is found using an expression above. | |||
== Comparison to Triangular Traction == | |||
While some a swayed that the use of exponential laws is somehow realistic while linear laws are too simplistic, the details of cohesive law shapes are of second-order importance. They have some minor effects (such as changes in predicted R curve shapes<ref name="czm"/>), but in general, any two laws with the same toughness (J<sub>c</sub>) and peak (σ<sub>c</sub>), will have very similar results. | |||
The only difference between this exponential law and the [[Triangular Traction Law]] is the α parameter. As shown in the figure above, this parameter changes the decay region of the cohesive law. If one does a series of simulations keeping J<sub>c</sub> and σ<sub>c</sub> constant, but varying α (as a consequence, δ<sub>c</sub> will increase as α increases), the results will have only minor differences. Because [[Triangular Traction Law]] is more efficient, it is usually the preferred cohesive law for simulations. This exponential law is provided for comparison to others or if the minor differences become important. | |||
== Failure == | |||
This laws uses uncoupled mode I and mode II cohesive laws. The failure is handled by the same methods used for the [[Triangular Traction Law]]. This exponential cohesive law can also be used for mode I or mode II laws in coupled mixed-mode modeling<ref name="mmzone"/> by using the [[Mixed Mode Traction Law]]. | |||
== Traction Law Properties == | |||
The following properties are used to create a triangular traction law: | |||
{| class="wikitable" | |||
|- | |||
! Property !! Description !! Units !! Default | |||
|- | |||
| alphaI || Mode I α coefficient || Dimensionless || none | |||
|- | |||
| alphaII || Mode II α coefficient || Dimensionless || none | |||
|- | |||
| ([[Triangular Traction Law#Traction Law Properties|other]]) || All other triangular traction law properties || varies || varies | |||
|} | |||
The resulting laws are required to have alphaI and alphaII greater than zero. | |||
== Traction History Variables == | |||
This material tracks two history variables: | |||
# Maximum normal opening displacement (or equal to normal δ<sub>e</sub> prior to initiation). | |||
# Maximum shear opening displacement magnitude (or equal to tangential δ<sub>e</sub> prior to initiation). | |||
These history variables can be [[MPM Archiving Options#ToArchive Command|archived]] for later plotting. The [[MPM Archiving Options#ToArchive Command|cmdisp archiving option]] can archive total mode I and mode II cumulative dissipated energies. | |||
== References == | |||
<references> | |||
<ref name="mmzone">J. A. Nairn and Y. E. Aimene "A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws" <i>in preparation</i> (2020).</ref> | |||
<ref name="czm">J. A. Nairn, "Analytical and Numerical Modeling of R Curves for Cracks with Bridging Zones" <i>Int. J. Fracture</i>, <b>155</b>, 167-181 (2009). ([http://www.cof.orst.edu/cof/wse/faculty/Nairn/papers/JBridging.pdf See PDF])</ref> | |||
</references> | |||
Latest revision as of 21:13, 2 January 2021
The Traction Law
This traction law assumes a linear elastic response up to σc followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δc. The exponential decay in the post peak region (i.e., δ>δe) is given by
[math]\displaystyle{ S(\delta) = \sigma_c\frac{e^{-\alpha\frac{\delta-\delta_e}{\delta_c-\delta_e}}-e^{-\alpha}}{1-e^{-\alpha}} }[/math]
This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II).
Notice how the shape changes with α. In the limit of α=0, this law is identical to the Triangular Traction Law (and that one should be used instead because it is more efficient). Increasing α causes traction to drop faster, which might simulate increasingly brittle response. The toughness of this cohesive law is the area under the curve that can be cast as
[math]\displaystyle{ J_c = {1\over 2} \sigma_c\delta_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right) \quad{\rm where}\quad f(\alpha) = 2\left(\frac{1}{\alpha}-\frac{e^{-\alpha}}{1-e^{-\alpha}}\right) }[/math]
and δpeak=δe/δc. The function f(α) is 1 when α=0 and decays to zero as α increases. The toughness is thus bracketed by
[math]\displaystyle{ {1\over 2} \sigma_c\delta_e \le J_c \le {1\over 2} \sigma_c\delta_c }[/math]
The minimum corresponds to large α with an instant drop to zero traction at δe while the maximum corresponds to α=0 and is area under the corresponding Triangular Traction Law.
When creating this traction law, you have to enter α, exactly two of σc, δpeak, and k and either Jc or δc. These four required properties must be entered for both mode I and mode II. If you enter δc, then the missing one of σc, δpeak, and k is calculated from one of
[math]\displaystyle{ k = {\sigma_c\over \delta_{peak}\delta_c} \qquad {\rm or} \qquad \delta_{peak} = {\sigma_c\over k\delta_c} \qquad {\rm or} \qquad \sigma_c = k \delta_{peak}\delta_c }[/math]
Finally Jc is found from the expression above. If instead you enter Jc, the calculation of δc depends on which two of σc, δpeak, and k are provided:
[math]\displaystyle{ {\rm from\ }\sigma_c\ {\rm and}\ \delta_{peak}:\quad \delta_c = \frac{2J_c}{\sigma_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right)} }[/math]
[math]\displaystyle{ {\rm from\ }\sigma_c\ {\rm and}\ k:\quad \delta_c = \frac{2kJ_c-\bigl(1-f(\alpha)\bigr)\sigma_c^2}{k\sigma_cf(\alpha)} }[/math]
[math]\displaystyle{ {\rm from\ }\delta_{peak}\ {\rm and}\ k:\quad \delta_c = \sqrt{\frac{2J_c}{k\delta_{peak}\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right)}} }[/math]
Once δc is found, the remaining property among σc, δpeak, and k is found using an expression above.
Comparison to Triangular Traction
While some a swayed that the use of exponential laws is somehow realistic while linear laws are too simplistic, the details of cohesive law shapes are of second-order importance. They have some minor effects (such as changes in predicted R curve shapes[1]), but in general, any two laws with the same toughness (Jc) and peak (σc), will have very similar results.
The only difference between this exponential law and the Triangular Traction Law is the α parameter. As shown in the figure above, this parameter changes the decay region of the cohesive law. If one does a series of simulations keeping Jc and σc constant, but varying α (as a consequence, δc will increase as α increases), the results will have only minor differences. Because Triangular Traction Law is more efficient, it is usually the preferred cohesive law for simulations. This exponential law is provided for comparison to others or if the minor differences become important.
Failure
This laws uses uncoupled mode I and mode II cohesive laws. The failure is handled by the same methods used for the Triangular Traction Law. This exponential cohesive law can also be used for mode I or mode II laws in coupled mixed-mode modeling[2] by using the Mixed Mode Traction Law.
Traction Law Properties
The following properties are used to create a triangular traction law:
| Property | Description | Units | Default |
|---|---|---|---|
| alphaI | Mode I α coefficient | Dimensionless | none |
| alphaII | Mode II α coefficient | Dimensionless | none |
| (other) | All other triangular traction law properties | varies | varies |
The resulting laws are required to have alphaI and alphaII greater than zero.
Traction History Variables
This material tracks two history variables:
- Maximum normal opening displacement (or equal to normal δe prior to initiation).
- Maximum shear opening displacement magnitude (or equal to tangential δe prior to initiation).
These history variables can be archived for later plotting. The cmdisp archiving option can archive total mode I and mode II cumulative dissipated energies.
References
- ↑ J. A. Nairn, "Analytical and Numerical Modeling of R Curves for Cracks with Bridging Zones" Int. J. Fracture, 155, 167-181 (2009). (See PDF)
- ↑ J. A. Nairn and Y. E. Aimene "A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws" in preparation (2020).