Difference between revisions of "Cubic Traction Law"
| (16 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== The Traction Law == | == The Traction Law == | ||
[[Cubictraction.jpg|right]] | [[File:Cubictraction.jpg|right]] | ||
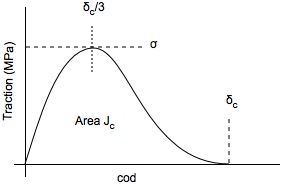
This [[Traction Laws|traction law]] assumes | This [[Traction Laws|traction law]] assumes use a cubic cohesive law for traction as a function of crack opening displacement (COD). The four parameters in the cubic function of found by requiring zero traction at δ=0 and at δ=δ<sub>c</sub>, peak stress at σ, and zero slope at δ=δ<sub>c</sub>. Note that the peek stress is always at δ<sub>c</sub>/3. This traction law was first proposed by Needleman.<ref name="cubic"/> It has a convenient smooth shape for numerical calculations and the zero slope at δ<sub>c</sub> may be desirable. There is no physical basis to claim it is more realistic than other traction laws. The resulting function is | ||
| |||
<math>\sigma = {27\over 4}\sigma_{max} {\delta\over\delta_c}\left(1-{\delta\over\delta_c}\right)^2</math> | |||
There are separate traction laws for opening displacement (mode I) and sliding displacement (mode II). | |||
The toughness of this traction law is the area under the curve or: | |||
| |||
<math>J_c = {9\over 16} \sigma\delta_c</math> | |||
When creating this traction law, you have to enter exactly two of these failure properties for both mode I and mode II (''i.e.'', two of J<sub>Ic</sub>, σ<sub>I</sub>, and δ<sub>Ic</sub> and two of J<sub>IIc</sub>, σ<sub>II</sub>, and δ<sub>IIc</sub>). Whichever property is not specified will be calculated from the two provided properties using one of the following relations: | |||
| |||
<math>\delta_c = {16J_c\over 9000\sigma}, \qquad \sigma = {16J_c\over 9000\delta_c}, \qquad {\rm or} \qquad J_c = {9000\over 16}\sigma\delta_c</math> | |||
These relations assume J<sub>Ic</sub> in J/m<sup>2</sup>, σ in [[ConsistentUnits Command#Legacy and Consistent Units|pressure units]], and δ<sub>c</sub> in [[ConsistentUnits Command#Legacy and Consistent Units|length units]]. | |||
Besides specifying area and toughness properties, the cubic traction law has no other adjustable parameters. The initial slope and peak location are given once the area is specified. Thus unlike most other [[Traction Laws|traction laws]], this law has fewer parameters, which can be helpful when studying role of traction laws on failure simulations. | |||
== Failure == | == Failure == | ||
This laws uses uncoupled mode I and mode II cohesive laws. The failure is handled by the same methods used for the [[Triangular Traction Law]]. This cubic cohesive law can also be used for mode I or mode II laws in coupled mixed-mode modeling<ref name="mmzone"/> by using the [[Mixed Mode Traction Law]]. | |||
== Traction Law Properties == | == Traction Law Properties == | ||
This traction law only needs the common traction law properties | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 18: | Line 39: | ||
| ([[Common Traction Law Properties|other]]) || Properties common to all traction laws || varies || varies | | ([[Common Traction Law Properties|other]]) || Properties common to all traction laws || varies || varies | ||
|} | |} | ||
== Traction History Variables == | |||
This material tracks two history variables: | |||
# Maximum normal opening displacement | |||
# Maximum shear opening displacement magnitude | |||
These history variables can be [[MPM Archiving Options#ToArchive Command|archived]] for later plotting. The [[MPM Archiving Options#ToArchive Command|cmdisp archiving option]] can archive total mode I and mode II cumulative dissipated energies. | |||
== References == | |||
<references> | |||
<ref name="mmzone">J. A. Nairn and Y. E. Aimene "A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws" <i>in preparation</i> (2020).</ref> | |||
<ref name="cubic">A. Needleman, "A continuum model for void nucleation by inclusion debonding," <i>J. Appl. Mech.</i>, <b>54</b>, 525–531. (1987)</ref> | |||
</references> | |||
Latest revision as of 21:14, 2 January 2021
The Traction Law
This traction law assumes use a cubic cohesive law for traction as a function of crack opening displacement (COD). The four parameters in the cubic function of found by requiring zero traction at δ=0 and at δ=δc, peak stress at σ, and zero slope at δ=δc. Note that the peek stress is always at δc/3. This traction law was first proposed by Needleman.[1] It has a convenient smooth shape for numerical calculations and the zero slope at δc may be desirable. There is no physical basis to claim it is more realistic than other traction laws. The resulting function is
[math]\displaystyle{ \sigma = {27\over 4}\sigma_{max} {\delta\over\delta_c}\left(1-{\delta\over\delta_c}\right)^2 }[/math]
There are separate traction laws for opening displacement (mode I) and sliding displacement (mode II).
The toughness of this traction law is the area under the curve or:
[math]\displaystyle{ J_c = {9\over 16} \sigma\delta_c }[/math]
When creating this traction law, you have to enter exactly two of these failure properties for both mode I and mode II (i.e., two of JIc, σI, and δIc and two of JIIc, σII, and δIIc). Whichever property is not specified will be calculated from the two provided properties using one of the following relations:
[math]\displaystyle{ \delta_c = {16J_c\over 9000\sigma}, \qquad \sigma = {16J_c\over 9000\delta_c}, \qquad {\rm or} \qquad J_c = {9000\over 16}\sigma\delta_c }[/math]
These relations assume JIc in J/m2, σ in pressure units, and δc in length units.
Besides specifying area and toughness properties, the cubic traction law has no other adjustable parameters. The initial slope and peak location are given once the area is specified. Thus unlike most other traction laws, this law has fewer parameters, which can be helpful when studying role of traction laws on failure simulations.
Failure
This laws uses uncoupled mode I and mode II cohesive laws. The failure is handled by the same methods used for the Triangular Traction Law. This cubic cohesive law can also be used for mode I or mode II laws in coupled mixed-mode modeling[2] by using the Mixed Mode Traction Law.
Traction Law Properties
This traction law only needs the common traction law properties
| Property | Description | Units | Default |
|---|---|---|---|
| (other) | Properties common to all traction laws | varies | varies |
Traction History Variables
This material tracks two history variables:
- Maximum normal opening displacement
- Maximum shear opening displacement magnitude
These history variables can be archived for later plotting. The cmdisp archiving option can archive total mode I and mode II cumulative dissipated energies.