Difference between revisions of "Comparison of Neo-Hookean Materials"
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | |||
== Introduction == | == Introduction == | ||
The definition of an isotropic, neo-Hookean is an elastic material that depends ot two elastic constants and in the limit of small deformations is identical to a [[Isotropic Material|small-strain, linear-elastic, Hookean material]]. The currently available [[Material Models|MPM Materials]] that a neo-Hookean material options are: | The definition of an isotropic, neo-Hookean material is an elastic material that depends ot two elastic constants and in the limit of small deformations is identical to a [[Isotropic Material|small-strain, linear-elastic, Hookean material]]. The currently available [[Material Models|MPM Materials]] that a neo-Hookean material options are: | ||
# [[Neo-Hookean Material]] | # [[Neo-Hookean Material]] | ||
# [[Mooney Material]] | # [[Mooney Material]] | ||
#* [[Isotropic, Hyperelastic-Plastic Material]] | |||
#* [[Isotropic, Hyperelastic-Plastic Mie-Grüneisen Material]] | |||
# [[Clamped Neo-Hookean Material]] | # [[Clamped Neo-Hookean Material]] | ||
The first is always a neo-Hookean material. The second has three properties for bulk modulus (K) and two shear modulus (G<sub>1</sub> and G<sub>2</sub>). | The first is always a neo-Hookean material. The second has three properties for bulk modulus (K) and two shear modulus (G<sub>1</sub> and G<sub>2</sub>). It can be considered as a neo-Hookeen material that reduces to small strain material with same bulk modulus and shear modulus G = G<sub>1</sub>+ G<sub>2</sub>. The subclasses of [[Mooney Material]] use elastic part of that material with G=G<sub>1</sub> abd G<sub>2</sub>=0. The [[Isotropic, Hyperelastic-Plastic Mie-Grüneisen Material]] has different elaastic behavior in compression (but not plotted here yet). The third allows plastic deformation by limiting the amount of elongation in tension or compression. By turning off the clamping, the [[Clamped Neo-Hookean Material|clamped neo-Hookean material]] represents a modified corotated elasticity law. | ||
== Elastic Energy Functions == | == Elastic Energy Functions == | ||
| Line 27: | Line 30: | ||
| | ||
<math>W = {\lambda\over 2}(J_E-1)^2 + G\sum_k (\lambda_k-1)^2</math><br> | <math>W = {\lambda\over 2}(J_E-1)^2 + G\sum_k (\lambda_k-1)^2</math><br> | ||
To use this neo-Hookean material, the material properties must set either <tt> CritComp</tt> or <tt> CritTens</tt> to less than zero and set <tt>Elastic</tt> | To use this neo-Hookean material, the material properties must set either <tt> CritComp</tt> or <tt> CritTens</tt> to less than zero and set <tt>Elastic</tt> to zero. | ||
</li> | </li> | ||
</ul> | </ul> | ||
| Line 33: | Line 36: | ||
== Stress Strain Response == | == Stress Strain Response == | ||
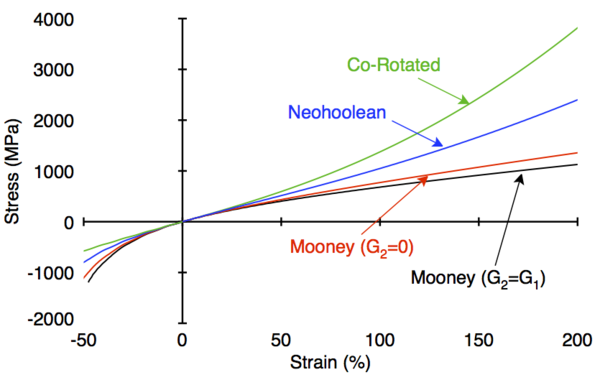
The following figure plots stress vs. strain from compression to tension for the above neo-Hookean materials. For the [[Mooney Material]], one plot uses G<sub>2</sub>=0 while the second uses G<sub>1</sub>=G<sub>2</sub>. Although all are the same in the small strain limit the differences | The following figure plots stress vs. strain from compression to tension for the above neo-Hookean materials. For the [[Mooney Material]], one plot uses G<sub>2</sub>=0 while the second uses G<sub>1</sub>=G<sub>2</sub>. Although all are the same in the small strain limit the differences at large strain are significant. The [[Mooney Material]] softens at high strain while the [[Neo-Hookean Material]] and [[Clamped Neo-Hookean Material]] (or "Co-Rotated" material) get stiffer at higher strain. The choice of material model should be based on corresponding response of an actual material. | ||
[[File: | [[File:NewHookean.png|center|600px]] | ||
Latest revision as of 17:09, 29 January 2023
Introduction
The definition of an isotropic, neo-Hookean material is an elastic material that depends ot two elastic constants and in the limit of small deformations is identical to a small-strain, linear-elastic, Hookean material. The currently available MPM Materials that a neo-Hookean material options are:
The first is always a neo-Hookean material. The second has three properties for bulk modulus (K) and two shear modulus (G1 and G2). It can be considered as a neo-Hookeen material that reduces to small strain material with same bulk modulus and shear modulus G = G1+ G2. The subclasses of Mooney Material use elastic part of that material with G=G1 abd G2=0. The Isotropic, Hyperelastic-Plastic Mie-Grüneisen Material has different elaastic behavior in compression (but not plotted here yet). The third allows plastic deformation by limiting the amount of elongation in tension or compression. By turning off the clamping, the clamped neo-Hookean material represents a modified corotated elasticity law.
Elastic Energy Functions
The elastic energy functions for these three material compared are:
- Neo-Hookean Material
[math]\displaystyle{ W ={\lambda\over 2 }({1\over 2 }(J^2-1)-\ln J) + {G\over 2 } (I_{1}-3-2\ln J) }[/math]
The first term can be changed to two other options to provide more neo-Hookean material models. - Mooney Material
[math]\displaystyle{ W ={\kappa\over 2 }({1\over 2 }(J^2-1)-\ln J) + {G_{1} \over 2 } (\bar I_{1}-3) + {G_{2} \over 2 }(\bar I_{2}-3) }[/math]
The first term can be changed to two other options to provide more neo-Hookean material models.This material is not strictly neo-Hookean (because of three material properties), but choosing G2=0 would make it a neo-Hookean material. If all parameters are used, it is neo-Hookean extension of small strain material with G = G1+G2. - Clamped Neo-Hookean Material
[math]\displaystyle{ W = {\lambda\over 2}(J_E-1)^2 + G\sum_k (\lambda_k-1)^2 }[/math]
To use this neo-Hookean material, the material properties must set either CritComp or CritTens to less than zero and set Elastic to zero.
Stress Strain Response
The following figure plots stress vs. strain from compression to tension for the above neo-Hookean materials. For the Mooney Material, one plot uses G2=0 while the second uses G1=G2. Although all are the same in the small strain limit the differences at large strain are significant. The Mooney Material softens at high strain while the Neo-Hookean Material and Clamped Neo-Hookean Material (or "Co-Rotated" material) get stiffer at higher strain. The choice of material model should be based on corresponding response of an actual material.