Difference between revisions of "Double Exponential Softening"
| (18 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | __TOC__ | ||
== The Softening Law == | == The Softening Law == | ||
The main goal of his [[Softening Laws|softening law]] is to provide another softening law that can initiate at low stress, <math>\sigma_{0}</math> (from the [[Damage Initiation Laws|damage initiation law]]), rise to a peak, <math>\sigma_0*f_{peak}</math>, and then decay. With that goal in mind, the function is | The main goal of his [[Softening Laws|softening law]] is to provide another softening law that can initiate at low stress, <math>\sigma_{0}</math> (from the [[Damage Initiation Laws|damage initiation law]]), rise to a peak, <math>\sigma_0*f_{peak}</math>, and then decay to zero. With that goal in mind, the function is | ||
| | ||
<math>f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right)</math> | <math>f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right)</math> | ||
where <math>\alpha>1</math> (to have second term decay faster) and <math>\beta<1</math> (to keep <math>f(\delta,s)>0</math>). The peak value of this function is located at: | [[File:DbleExp.png|500px|right]] | ||
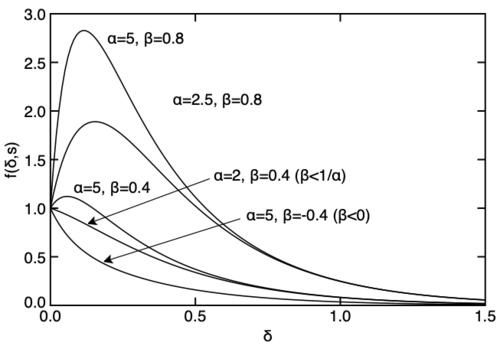
where <math>\alpha>1</math> (to have second term decay faster) and <math>\beta<1</math> (to keep <math>f(\delta,s)>0</math>). The figure on the right shows double exponential softening functions for various values of <math>\alpha</math> and <math>\beta</math>. The law peaks whenever <math>1/\alpha<\beta<1</math>. This behavior is valid for softening laws provided the modulus still monotonically softens (which is does for any valid parameters). The peak value of this function is located at: | |||
| | ||
| Line 19: | Line 21: | ||
\frac{\alpha-1}{\alpha(1-\beta)(\alpha\beta)^{\frac{1}{\alpha-1}}} & 1/\alpha<\beta<1 \\ | \frac{\alpha-1}{\alpha(1-\beta)(\alpha\beta)^{\frac{1}{\alpha-1}}} & 1/\alpha<\beta<1 \\ | ||
1 & \beta \le 1/\alpha \end{array}\right.</math> | 1 & \beta \le 1/\alpha \end{array}\right.</math> | ||
When using this law, you enter the initiation stress into the [[Damage Initiation Laws|initiation law]]. If you want to set the peak stress instead, the initiation stress should be reduced from that peak stress by this value of <math>f_{peak}</math>. When <math>\beta<1/\alpha</math>, this law monotonically decreases from 1 to 0. For <math>\beta<0</math>, this law is a simple double-exponential decay function. | |||
The value for <math>k</math> is is found from | The value for <math>k</math> is is found from | ||
| | ||
<math>sG_c = \int_0^{\infty} f(\delta,s) = \frac{\alpha-\beta}{k\alpha(1-\beta) | <math>sG_c = \int_0^{\infty} f(\delta,s) = \frac{\alpha-\beta}{k\alpha(1-\beta)} | ||
\quad{\rm or}\quad k = \frac{\alpha-\beta}{\alpha(1-\beta)sG_c}</math> | \quad{\rm or}\quad k = \frac{\alpha-\beta}{\alpha(1-\beta)sG_c}</math> | ||
| Line 29: | Line 33: | ||
The decay rate, <math>k</math>, which depends on mesh size and crack orientation, is calculated from ''s'' and ''G<sub>c</sub>'' and is not a law property to be provided. | The decay rate, <math>k</math>, which depends on mesh size and crack orientation, is calculated from ''s'' and ''G<sub>c</sub>'' and is not a law property to be provided. | ||
[[File: | [[File:DbleExpEtaRel.png|right]] | ||
The stability factor depends on relative values of <math>\alpha</math> and <math>\beta</math>: | The stability factor depends on relative values of <math>\alpha</math> and <math>\beta</math>: | ||
| Line 42: | Line 44: | ||
</math> | </math> | ||
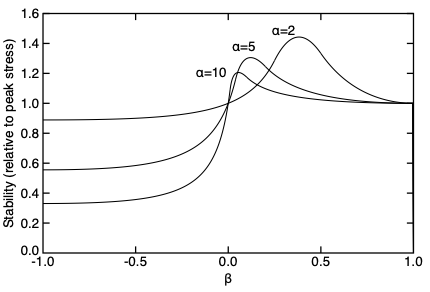
For <math>\beta=0</math>, the stability factor simplifies to <math>\eta = 1</math> which is identical to [[Exponential Softening]] (in fact the entire law is identical to [[Exponential Softening]] and that law should therefore be used instead). | For <math>\beta=0</math>, the stability factor simplifies to <math>\eta = 1</math> which is identical to [[Exponential Softening]] (in fact the entire law is identical to [[Exponential Softening]] and that law should therefore be used instead). Although this stability factor goes to zero as <math>\beta\to1</math>, the ''effective'' stability is better compared to monotonically decreasing laws by multiplying <math>\eta</math> by its peak value squared (''i.e.'', [[Softening Laws#Law Stability|minimum cell size]] is related to <math>\eta/\sigma_0^2</math> and <math>\sigma_0</math> decreases if set by reducing peak stress by <math>f_{peak}</math>). The figure on the right plots this ''effective'' stability factor as a function of <math>\beta</math> for various values of <math>\alpha</math>. For <math>\beta>0</math>, this law is slightly more stable than [[Exponential Softening]]. For <math>\beta<0</math>, this law decreases in stability as <math>\alpha</math> increases, because the second exponential term causes magnitude of the initial slope to increase. Using this law with <math>\beta<0</math> and a large <math>\alpha</math> may cause stability problems. Typically, this law should set <math>0<\beta<1</math> for which ''effective'' stability will range from 1 to 1.49. | ||
=== Minimum <math>f(\delta,s)</math> === | |||
This law requires selection of minimum value for <math>f(\delta,s)</math> below which the material point is marked as failed. If we define the minimum value as ''c'', this choice defines an effective maximum cracking strain by numerically solving for | |||
| |||
<math>f(\delta_{max},c) = c </math> | |||
Without a minimum value, double exponential softening would never fail. If you want to prevent failures, set the minimum value to a very small number (but it cannot be zero). | |||
== Softening Law Properties == | == Softening Law Properties == | ||
A double exponential softening law has four parameters (three of much must always be provided): | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 54: | Line 65: | ||
| Gc || The toughness associated with the this softening law || [[ConsistentUnits Command#Legacy and Consistent Units|energy release units]] || none | | Gc || The toughness associated with the this softening law || [[ConsistentUnits Command#Legacy and Consistent Units|energy release units]] || none | ||
|- | |- | ||
| | | alpha || relative decay rate of the second exponential (must be greater than 1) || none || none | ||
|- | |||
| beta || relative magnitude of the the second exponential (must be less than 1) || none || none | |||
|- | |||
| min || Minimum <math>f(\delta,s)</math> or law is failed if it gets below this value || none || 0.01 | |||
|} | |} | ||
Latest revision as of 19:57, 29 January 2023
The Softening Law
The main goal of his softening law is to provide another softening law that can initiate at low stress, [math]\displaystyle{ \sigma_{0} }[/math] (from the damage initiation law), rise to a peak, [math]\displaystyle{ \sigma_0*f_{peak} }[/math], and then decay to zero. With that goal in mind, the function is
[math]\displaystyle{ f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right) }[/math]
where [math]\displaystyle{ \alpha\gt 1 }[/math] (to have second term decay faster) and [math]\displaystyle{ \beta\lt 1 }[/math] (to keep [math]\displaystyle{ f(\delta,s)\gt 0 }[/math]). The figure on the right shows double exponential softening functions for various values of [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]. The law peaks whenever [math]\displaystyle{ 1/\alpha\lt \beta\lt 1 }[/math]. This behavior is valid for softening laws provided the modulus still monotonically softens (which is does for any valid parameters). The peak value of this function is located at:
[math]\displaystyle{ \delta_{peak} = \left\{ \begin{array}{ll} \frac{ \ln \alpha\beta }{k(\alpha-1)} & 1/\alpha\lt \beta\lt 1 \\ 0 & \beta \le 1/\alpha \end{array}\right. }[/math]
The corresponding peak value is:
[math]\displaystyle{ f_{peak} = \left\{ \begin{array}{ll} \frac{\alpha-1}{\alpha(1-\beta)(\alpha\beta)^{\frac{1}{\alpha-1}}} & 1/\alpha\lt \beta\lt 1 \\ 1 & \beta \le 1/\alpha \end{array}\right. }[/math]
When using this law, you enter the initiation stress into the initiation law. If you want to set the peak stress instead, the initiation stress should be reduced from that peak stress by this value of [math]\displaystyle{ f_{peak} }[/math]. When [math]\displaystyle{ \beta\lt 1/\alpha }[/math], this law monotonically decreases from 1 to 0. For [math]\displaystyle{ \beta\lt 0 }[/math], this law is a simple double-exponential decay function.
The value for [math]\displaystyle{ k }[/math] is is found from
[math]\displaystyle{ sG_c = \int_0^{\infty} f(\delta,s) = \frac{\alpha-\beta}{k\alpha(1-\beta)} \quad{\rm or}\quad k = \frac{\alpha-\beta}{\alpha(1-\beta)sG_c} }[/math]
Here s is the softening scaling term and Gc is toughness of the law. The decay rate, [math]\displaystyle{ k }[/math], which depends on mesh size and crack orientation, is calculated from s and Gc and is not a law property to be provided.
The stability factor depends on relative values of [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]:
[math]\displaystyle{ \eta = \left\{ \begin{array}{ll} \frac{\alpha^2(1-\beta)^2(\alpha^2\beta)^{\frac{1}{\alpha-1}}}{(\alpha-\beta)(\alpha-1)} & {\rm for\ } \beta\gt 1/\alpha^2 \\ \frac{\alpha(1-\beta)^2}{(\alpha-\beta)(1-\alpha\beta)} & {\rm for\ } \beta \lt 1/\alpha^2 \end{array}\right. }[/math]
For [math]\displaystyle{ \beta=0 }[/math], the stability factor simplifies to [math]\displaystyle{ \eta = 1 }[/math] which is identical to Exponential Softening (in fact the entire law is identical to Exponential Softening and that law should therefore be used instead). Although this stability factor goes to zero as [math]\displaystyle{ \beta\to1 }[/math], the effective stability is better compared to monotonically decreasing laws by multiplying [math]\displaystyle{ \eta }[/math] by its peak value squared (i.e., minimum cell size is related to [math]\displaystyle{ \eta/\sigma_0^2 }[/math] and [math]\displaystyle{ \sigma_0 }[/math] decreases if set by reducing peak stress by [math]\displaystyle{ f_{peak} }[/math]). The figure on the right plots this effective stability factor as a function of [math]\displaystyle{ \beta }[/math] for various values of [math]\displaystyle{ \alpha }[/math]. For [math]\displaystyle{ \beta\gt 0 }[/math], this law is slightly more stable than Exponential Softening. For [math]\displaystyle{ \beta\lt 0 }[/math], this law decreases in stability as [math]\displaystyle{ \alpha }[/math] increases, because the second exponential term causes magnitude of the initial slope to increase. Using this law with [math]\displaystyle{ \beta\lt 0 }[/math] and a large [math]\displaystyle{ \alpha }[/math] may cause stability problems. Typically, this law should set [math]\displaystyle{ 0\lt \beta\lt 1 }[/math] for which effective stability will range from 1 to 1.49.
Minimum [math]\displaystyle{ f(\delta,s) }[/math]
This law requires selection of minimum value for [math]\displaystyle{ f(\delta,s) }[/math] below which the material point is marked as failed. If we define the minimum value as c, this choice defines an effective maximum cracking strain by numerically solving for
[math]\displaystyle{ f(\delta_{max},c) = c }[/math]
Without a minimum value, double exponential softening would never fail. If you want to prevent failures, set the minimum value to a very small number (but it cannot be zero).
Softening Law Properties
A double exponential softening law has four parameters (three of much must always be provided):
| Property | Description | Units | Default |
|---|---|---|---|
| Gc | The toughness associated with the this softening law | energy release units | none |
| alpha | relative decay rate of the second exponential (must be greater than 1) | none | none |
| beta | relative magnitude of the the second exponential (must be less than 1) | none | none |
| min | Minimum [math]\displaystyle{ f(\delta,s) }[/math] or law is failed if it gets below this value | none | 0.01 |