Detecting Contact

Both multimaterial mode MPM and explicit cracks need to detect when two surfaces are in contact. This page describes the contact detection options.

Basic Contact Detection

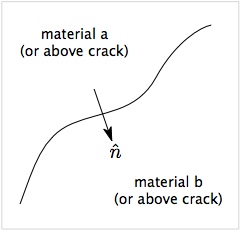
The figure shows a surface between two materials (a and b) or between two sides of a crack (above and below). The arrow shows a vector normal to the surface oriented from side a to side b. For both multimaterial contact and crack contact, the first step is to decide if the two velocity fields at the node are actually in contact. NairnMPM uses two (or more) criteria to detect contact.

Approach velocity

The first step is to decide the two surface are approaching each other in the normal direction. This criterion reduces to       [math]\displaystyle{ \Delta\vec v \cdot \hat n \lt 0 \qquad {\rm where} \qquad \Delta\vec v = \vec v_a - \vec v_b }[/math] When this criterion is not satisfied, the surfaces are separating and assumed to not be in contact. In early multimaterial MPM, when this criterion is satisfied, the surfaces were assume to be in contact. It is easy to visualize, however, that this approach detects contact when surfaces are just are approaching each other but still separated. For improved contact, a second criterion based on displacements is added.

Displacement check

If the approach velocity criterion is satisfied, NairnMPM next looks at displacements or positions of the two velocity fields. Basically, this criterion calculates the location of the two surfaces. If the overlap in the normal direction the surfaces are in contact. If they are separated, the surfaces are not in contact. There are two ways to find crack surfaces from displacements or positiong in velocity fields; these methods are described in the section on the ContactPosition.

Both multimaterial mode contact and crack contact use the above two criterion, but they have some other options. For example, the displacement check is optional in multimaterial mode but is always done for crack contact. In addition, multimaterial mode has an optional screening criterion based on nodal volume that can help screen out nodes that are likely to cause numerical inaccuracies. See the sections below for details.

Notes

1. An accurate normal vector is crucial to contact detection and contact physics. The methods for calculating these normals is described here.
2. Since the displacement check seems to track contact best, why not skip the approach velocity criterion? The answer is that the algorithms used to adjust nodal momementum for some contact physics (e.g., friction) do not make physical sense unless that criterion is satisfied.

Multimaterial Mode Contact Detection

The first step is to decide if the materials at the node are actually in contact. NairnMPM allows a simulation to use various combinations of the following three contact detection criteria:

1. If the total volume at the node is less than some fraction of the total volume expected for an internal node (a parameter Vmin), the materials at that node are assumed to not be in contact. If the volume is greater than Vmin, the contact detection continues. This check can be skipped by setting Vmin = 0 (because all nodes with materials will have volume greater than zero).
2. Next, the normal to the material contact surface is calculated and it is used to determine the velocity of approach for the two material surfaces. If the surfaces are moving apart, the node is assumed to not be in contact. If they are moving toward each other, the contact detection continues.
3. Finally, if enabled, the displacements for each material at the node are calculated. If the two materials overlap, the node is in contact. If not, the node is assumed to not be in contact. There are two ways to find displacements. The method is selected with the ContactPosition command (where details on the methods are given).