Difference between revisions of "Triangular Traction Law"
| Line 4: | Line 4: | ||
[[File:Tritraction.jpg|right]] | [[File:Tritraction.jpg|right]] | ||
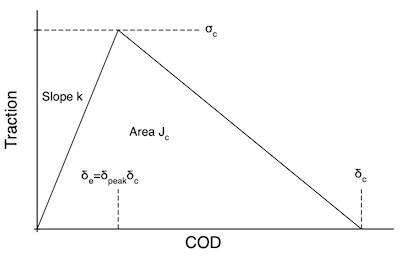
This [[Traction Laws|traction law]] | This [[Traction Laws|traction law]] assumes the triangular shape for traction as a function of crack opending displacement (COD). There are separate traction laws for opening displacement (mode I) and sliding displacement (mode II). | ||
The toughness of this traction law is the area under the curve or: | The toughness of this traction law is the area under the curve or: | ||
| Line 11: | Line 11: | ||
<math>J_c = {1\over 2} \sigma\delta_c</math> | <math>J_c = {1\over 2} \sigma\delta_c</math> | ||
When creating this traction law, you have to enter exactly two of these failure properties for both mode I and mode II (i.e., two of J<sub>Ic</sub>, σ<sub>I</sub>, and δ<sub>Ic</sub> and two of J<sub>IIc</sub>, σ<sub>II</sub>, and δ<sub>IIc</sub>). Whichever property is not specified will be calculated from the | When creating this traction law, you have to enter exactly two of these failure properties for both mode I and mode II ''(i.e.'', two of J<sub>Ic</sub>, σ<sub>I</sub>, and δ<sub>Ic</sub> and two of J<sub>IIc</sub>, σ<sub>II</sub>, and δ<sub>IIc</sub>). Whichever property is not specified will be calculated from the two provided properties using one of the following relations: | ||
| | ||
| Line 18: | Line 18: | ||
These relations assume J<sub>Ic</sub> in J/m<sup>2</sup>, σ in MPa, and δ<sub>c</sub> in mm. | These relations assume J<sub>Ic</sub> in J/m<sup>2</sup>, σ in MPa, and δ<sub>c</sub> in mm. | ||
To get the initial rise and location of the peak, you can provide, k, and the relative crack opening displacement at the peak stress, δ<sub>peak</sub> ( | To get the initial rise and location of the peak, you can provide, k, and the relative crack opening displacement at the peak stress, δ<sub>peak</sub> (which is entered is relative to the critical opening displacement or the COD at the peak is δ<sub>peak</sub>δ<sub>c</sub>). You must enter zero or one of these terms above for both mode I and mode II (''i.e.'', zero or one of k<sub>Ie</sub> and δ<sub>I,peak</sub> and zero or one of k<sub>IIe</sub> and δ<sub>II,peak</sub>). If one is provided, the other will be calculated from: | ||
| | ||
<math>k = {\sigma\over \delta_{peak}\delta_c}</math> | <math>k = {\sigma\over \delta_{peak}\delta_c} \qquad {\rm or} \qquad \delta_{peak} = {\sigma\over k\delta_c} </math> | ||
If neither k nor δ<sub>peak</sub> are entered, the peak will be located at δ<sub>peak</sub> = 0.225926299. This location provides the closest match to the [[Cubic Traction Law|cubic traction law] for area under the curve as a function of | If neither k nor δ<sub>peak</sub> are entered, the peak will be located at δ<sub>peak</sub> = 0.225926299. This location provides the closest match to the [[Cubic Traction Law|cubic traction law]] for area under the curve as a function of COD. The initial slope will be set to | ||
| | ||
<math>k = {\sigma\over 0.225926299 \delta_c}</math> | <math>k = {\sigma\over 0.225926299 \delta_c}</math> | ||
== Failure == | |||
The entered traction laws give mode I or mode II traction law for pure mode I or pure mode II loading. Under pure mode lode, the traction law will fail (and release the crack surfaces) when the COD reaches the critical COD ()δ<sub>c</sub> for that mode. | |||
For mixed-mode loading, the normal and and shear tractions still depend only on normal and shear displacements, respectively, but the conditions for failure change. For mixed-mode loading, failure occurs when: | |||
| | ||
<math>\left({G_I\over J_{Ic}}\right)^{n} + \left({G_{II}\over J_{IIc}}\right)^{n} = 1</math> | <math>\left({G_I\over J_{Ic}}\right)^{n} + \left({G_{II}\over J_{IIc}}\right)^{n} = 1</math> | ||
where G<sub>I</sub> and G<sub>II</sub> are areas under mode I and mode II traction laws up to current | where G<sub>I</sub> and G<sub>II</sub> are areas under mode I and mode II traction laws up to current COD and ''n'' is mixed-mode failure criterion parameter. This failure criterion will mean that failure may occur when normal or shear tractions are nonzero. In other words, each traction law will have COD less then their critical COD, which means their traction will be greater than zero. Because failure released the crack surface, mixed-mode failure by this criterion may result in a sudden drop of finite normal and shear traction to zero traction. This approach is identical to the one adopted by Thouless ''et. al'' to handle mixed-mode loading and appears to work well. | ||
There has been work to modify the traction laws so they always approach zero at time of failure (e.g., work of Hogberg (2006) or Tvergaard and Hutchinson (1994)). These approaches were tried, gave poor results for certain problems, led to non-physical coupling between mode I and mode II, and therefore are not recommended. The [[Coupled Traction Law|coupled traction law]] available in [[NairnMPM]] lets you try a law that couples to COD such that failure occurs when tractions drop to zero. | |||
== Traction Law Properties == | == Traction Law Properties == | ||
| Line 58: | Line 60: | ||
|} | |} | ||
To get pure linear softening (i.e, peak at zero COD with linear decrease to the critical | To get pure linear softening (i.e, peak at zero COD with linear decrease to the critical COD), you can enter zero for delpkI or delpkII of either mode. Although a pure linear softening law is allowed, experience suggest that having an initial elastic region before the peak with finite slope (kIe or kIIe less then ∞) works better. Thus if you experience problems with a pure linear softening law, the solution might be to increase the peak position to make the initial stiffness finite. | ||
Revision as of 11:43, 7 January 2014
The Traction Law
This traction law assumes the triangular shape for traction as a function of crack opending displacement (COD). There are separate traction laws for opening displacement (mode I) and sliding displacement (mode II).
The toughness of this traction law is the area under the curve or:
[math]\displaystyle{ J_c = {1\over 2} \sigma\delta_c }[/math]
When creating this traction law, you have to enter exactly two of these failure properties for both mode I and mode II (i.e., two of JIc, σI, and δIc and two of JIIc, σII, and δIIc). Whichever property is not specified will be calculated from the two provided properties using one of the following relations:
[math]\displaystyle{ \delta_c = {J_c\over 500\sigma}, \qquad \sigma = {J_c\over 500\delta_c}, \qquad {\rm or} \qquad J_c = 500\sigma\delta_c }[/math]
These relations assume JIc in J/m2, σ in MPa, and δc in mm.
To get the initial rise and location of the peak, you can provide, k, and the relative crack opening displacement at the peak stress, δpeak (which is entered is relative to the critical opening displacement or the COD at the peak is δpeakδc). You must enter zero or one of these terms above for both mode I and mode II (i.e., zero or one of kIe and δI,peak and zero or one of kIIe and δII,peak). If one is provided, the other will be calculated from:
[math]\displaystyle{ k = {\sigma\over \delta_{peak}\delta_c} \qquad {\rm or} \qquad \delta_{peak} = {\sigma\over k\delta_c} }[/math]
If neither k nor δpeak are entered, the peak will be located at δpeak = 0.225926299. This location provides the closest match to the cubic traction law for area under the curve as a function of COD. The initial slope will be set to
[math]\displaystyle{ k = {\sigma\over 0.225926299 \delta_c} }[/math]
Failure
The entered traction laws give mode I or mode II traction law for pure mode I or pure mode II loading. Under pure mode lode, the traction law will fail (and release the crack surfaces) when the COD reaches the critical COD ()δc for that mode.
For mixed-mode loading, the normal and and shear tractions still depend only on normal and shear displacements, respectively, but the conditions for failure change. For mixed-mode loading, failure occurs when:
[math]\displaystyle{ \left({G_I\over J_{Ic}}\right)^{n} + \left({G_{II}\over J_{IIc}}\right)^{n} = 1 }[/math]
where GI and GII are areas under mode I and mode II traction laws up to current COD and n is mixed-mode failure criterion parameter. This failure criterion will mean that failure may occur when normal or shear tractions are nonzero. In other words, each traction law will have COD less then their critical COD, which means their traction will be greater than zero. Because failure released the crack surface, mixed-mode failure by this criterion may result in a sudden drop of finite normal and shear traction to zero traction. This approach is identical to the one adopted by Thouless et. al to handle mixed-mode loading and appears to work well.
There has been work to modify the traction laws so they always approach zero at time of failure (e.g., work of Hogberg (2006) or Tvergaard and Hutchinson (1994)). These approaches were tried, gave poor results for certain problems, led to non-physical coupling between mode I and mode II, and therefore are not recommended. The coupled traction law available in NairnMPM lets you try a law that couples to COD such that failure occurs when tractions drop to zero.
Traction Law Properties
The following properties are used to create a triangular traction law:
| Property | Description | Units | Default |
|---|---|---|---|
| kIe | Initial elastic slope, k in mode I | MPa/mm | none |
| delpkI | COD for peak stress, δpeak, relative to critical COD in mode I (0 to 1) | dimensionless | none |
| kIIe | Initial elastic slope, k in mode I | MPa/mm | none |
| delpkII | COD for peak stress, δpeak, relative to critical COD in mode II (0 to 1) | dimensionless | none |
| (other) | Properties common to all traction laws | varies | varies |
To get pure linear softening (i.e, peak at zero COD with linear decrease to the critical COD), you can enter zero for delpkI or delpkII of either mode. Although a pure linear softening law is allowed, experience suggest that having an initial elastic region before the peak with finite slope (kIe or kIIe less then ∞) works better. Thus if you experience problems with a pure linear softening law, the solution might be to increase the peak position to make the initial stiffness finite.