Difference between revisions of "Double Exponential Softening"
| Line 6: | Line 6: | ||
<math>f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right)</math> | <math>f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right)</math> | ||
where <math>\alpha>1</math> (to have second term decay faster) and <math>\beta<1</math> (to keep <math>f(\delta,s)>0</math>. The peak value of this function is located at: | where <math>\alpha>1</math> (to have second term decay faster) and <math>\beta<1</math> (to keep <math>f(\delta,s)>0</math>). The peak value of this function is located at: | ||
| | ||
| Line 13: | Line 13: | ||
0 & \beta \le 1/\alpha \end{array}\right.</math> | 0 & \beta \le 1/\alpha \end{array}\right.</math> | ||
The corresponding peak | The corresponding peak value is: | ||
| | ||
| Line 20: | Line 20: | ||
1 & \beta \le 1/\alpha \end{array}\right.</math> | 1 & \beta \le 1/\alpha \end{array}\right.</math> | ||
The value for <math>k</math> is is found from | |||
<math> | |||
| | ||
<math>sG_c = \int_0^{\ | <math>sG_c = \int_0^{\infty} f(\delta,s) = \frac{\alpha-\beta}{k\alpha(1-\beta)s} | ||
\quad{\rm or}\quad | \quad{\rm or}\quad k = \frac{\alpha-\beta}{\alpha(1-\beta)sG_c}</math> | ||
Here ''s'' is the [[Softening Laws#Normalized Softening Law|softening scaling term]] and ''G<sub>c</sub>'' is toughness of the law. | Here ''s'' is the [[Softening Laws#Normalized Softening Law|softening scaling term]] and ''G<sub>c</sub>'' is toughness of the law. | ||
The | The decay rate, <math>k</math>, which depends on mesh size and crack orientation, is calculated from ''s'' and ''G<sub>c</sub>'' and is not a law property to be provided. | ||
[[File:CubicStep.png|right]] | [[File:CubicStep.png|right]] | ||
Revision as of 09:51, 20 July 2021
The Softening Law
The main goal of his softening law is to provide another softening law that can initiate at low stress, [math]\displaystyle{ \sigma_{0} }[/math] (from the damage initiation law), rise to a peak, [math]\displaystyle{ \sigma_0*f_{peak} }[/math], and then decay. With that goal in mind, the function is
[math]\displaystyle{ f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right) }[/math]
where [math]\displaystyle{ \alpha\gt 1 }[/math] (to have second term decay faster) and [math]\displaystyle{ \beta\lt 1 }[/math] (to keep [math]\displaystyle{ f(\delta,s)\gt 0 }[/math]). The peak value of this function is located at:
[math]\displaystyle{ \delta_{peak} = \left\{ \begin{array}{ll} \frac{ \ln \alpha\beta }{k(\alpha-1)} & 1/\alpha\lt \beta\lt 1 \\ 0 & \beta \le 1/\alpha \end{array}\right. }[/math]
The corresponding peak value is:
[math]\displaystyle{ \sigma_{peak} = \left\{ \begin{array}{ll} \frac{\alpha-1}{\alpha(1-\beta)(\alpha\beta)^{\frac{1}{\alpha-1}}} & 1/\alpha\lt \beta\lt 1 \\ 1 & \beta \le 1/\alpha \end{array}\right. }[/math]
The value for [math]\displaystyle{ k }[/math] is is found from
[math]\displaystyle{ sG_c = \int_0^{\infty} f(\delta,s) = \frac{\alpha-\beta}{k\alpha(1-\beta)s} \quad{\rm or}\quad k = \frac{\alpha-\beta}{\alpha(1-\beta)sG_c} }[/math]
Here s is the softening scaling term and Gc is toughness of the law. The decay rate, [math]\displaystyle{ k }[/math], which depends on mesh size and crack orientation, is calculated from s and Gc and is not a law property to be provided.
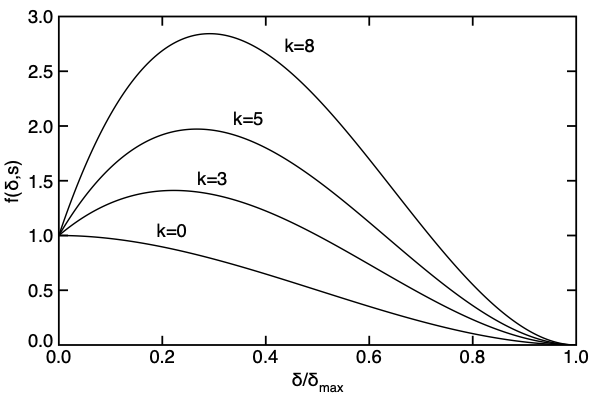
If [math]\displaystyle{ k=0 }[/math], this law is a cubic step function with [math]\displaystyle{ f'(0)=0 }[/math], but if [math]\displaystyle{ k\gt 0 }[/math], this function rises to a peak and then decays to failure at [math]\displaystyle{ \delta_{max} }[/math] (see plots on the right). This behavior is valid for softening laws provided the modulus still monotonically softens. When using [math]\displaystyle{ k\gt 0 }[/math], you enter the initial stress into the initiation law. If you want to set the peak stress, the initiation stress should be calculated from the desired peak using:
[math]\displaystyle{ \sigma_{0} = \frac{\left(1+\frac{k}{2}\right)^2}{\left(1+\frac{k}{3}\right)^3}\sigma_{peak} }[/math]
The area (or energy dissipation term) is
[math]\displaystyle{ \Omega(\delta,s) = {\delta \over 2} \left(1+\left({\delta\over \delta_{max}}\right)^2\left(\frac{4k_2-1}{3}-k_2{\delta\over \delta_{max}}\right)\right) }[/math]
The stability factor is:
[math]\displaystyle{ \eta = \frac{12k_2}{(1+2k_2)^2k_6} }[/math]
If [math]\displaystyle{ k=0 }[/math], the stability factor simplifies to [math]\displaystyle{ \eta = 4/3 }[/math], or slightly less stable than a linear softening law. As [math]\displaystyle{ k }[/math] increases the stability decreases. A difference between this law and linear softening law is that [math]\displaystyle{ f'(\delta_{max})=0 }[/math]. Thus, despite a reduction in stability, it is possible this zero derivative could reduce numerical effects caused by decohesions.
Softening Law Properties
Only one property is needed to define a cubic step function softening law:
| Property | Description | Units | Default |
|---|---|---|---|
| Gc | The toughness associated with the this softening law | energy release units | none |
| k | Initial slope of the law (must be nonnegative) (OSParticulas only) | none | 0 |