Crack Propagation Commands

The Crack Settings on this page activate crack propagation and select various propagation options.

Propagate Command

Simulations with crack propagation requires two setup tasks. First, when defining the cracks you must set the crack tip material for any crack tip that should propagate to be the material containing that tip. Crack tips without a material will not propagate. Second, you must use the Propagate command to set the default crack propagation properties. In scripted files, the command is

Propagate (crit),<(dir)>,<(traction)>

In XML files, the command, which must be in the <Cracks> block, is:

<Propagate criterion='(critNum)' direction='(dirNum)' traction='(traction)'/>

where (crit) and optionally (dir) are the crack propagation criterion and the method to select the crack propagation direction. The optional (traction) allows the crack to leave a traction law or cohesive zone in the wake of propagation. Finally see the section on crack tip materials for details on material properties and options for customizing crack propagation properties in simulations with more than one material.

Crack Propagation Criterion

The crack propagation criterion is one of the following options (which can be set by number or name, although XML files must use a number):

• 0:"none" for no propagation.
• 1:"max energy release" for crack growth based on stress intensity factors and a single critical stress intensity factor (K_Ic). The propagation condition is based on the maximum energy release rate (also known as the maximum hoop stress criterion). The default propagation direction is in the direction of maximum mode I or the direction of maximum hoop stress).
• 2:"steady state" for crack initiation when total energy release rate (J) reaches a critical value (specified by J_Ic) or when the time reaches a specified time (specified by initTime). Once the crack has initiated, the crack grows at a specified constant speed. It may be stopped at any predetermined maximum length. The default propagation direction is self-similar propagation.
• 3:"energy balance" for crack growth by a dynamic energy balancing scheme. The research for this option is in progress and it is not yet meant for general use. The default propagation direction is self-similar propagation.
• 4:"energy density" for crack growth based on stress intensity factors and a single critical stress intensity factor (K_Ic). The propagation condition is based on the minimum strain energy density. The default propagation direction is in the direction of minimum strain energy density.
• 5:"elliptical" for crack growth based on stress intensity factors and two critical stress intensity factors (K_Ic and K_IIc). The default propagation direction is the direction of maximum hoop stress. The criterion for crack growth is
  
        [math]\displaystyle{ \left({K_I\over K_{Ic}}\right)^p + \left({K_{II}\over K_{IIc}}\right)^q = 1 }[/math]
  
  
• 6:"max ctod" for crack growth if the normal or tangential crack tip opening displacement at the crack tip exceeds δ_Ic or δ_IIc, respectively, if one or both are specified. The default propagation direction is self-similar propagation.
• 7:"critical err" for crack growth when total energy release rate (J) exceeds the critical toughness J_Ic. The default propagation direction is self-similar propagation.

Crack Propagation Direction

Each crack propagation criterion has a default method for determination of the crack propagation direction. If desired, that direction can be changed using the optional (dir) parameter using one of the following options (which can be set by number or name, although XML files must use a number):

• 0:"default" to use the default direction for the bove criterion.
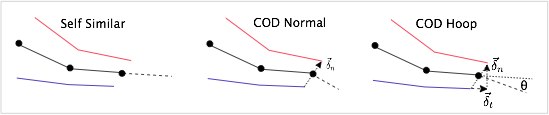
• 1:"self similar" to grow in the same direction as the crack tip crack segment.
• 2:"cod normal" to grow normal to a crack opening displacement vector between the top and bottom surface at the crack tip.
• 3:"cod hoop" to estimate the direction of maximum mode I based on the normal and shear crack opening displacements. This direction is similar to the maximum hoop stress direction, but can be used on any type of material.
• 4:"initial" to grow in the crack tip direction defined by the initial crack geometry.

The following figure illustrates the above crack propagation directions. Each one shows a crack plane in black that is defined by a series of crack particles connected the crack segments. The read and blue lines are the tracked crack surfaces above and below the crack plane. The dashed line show the direction of propagation. The vector δ is the crack opening displacement. The vectors δ_n and δ_t are the components of the crack opening displacement normal and tangential to the last crack segment. The propagation angle θ for "cod hoop" is calculated using the maximum hoop direction method. The "initial" direction is not shown because it depends on the crack position at the start of the simulation and not the current crack orientation or stress state.

Besides the above crack propagation direction options, NairnMPM has two other direction options that are tied to specific failure criteria. The maximum hoop direction method is tied to the "max energy release" and "elitpitcal" methods. This direction is selected by using one of these criteria along with their default propagation direction. Similarly, the minimum strain energy density direction is selected by using the "energy density" fracture criterion along with its default propagation direction. These two direction methods can only be used with these three fracture criteria because like those criteria, thy can only be used with isotropic crack tip materials.

Maximum Hoop Stress Direction

In the maximum hoop direction method, the crack direction is determined by the direction of maximum hoop stress (using polar stresses with the crack tip at the origin). This direction is found from the crack-tip stress state for a linear elastic, isotropic material. This direction also corresponds to the direction with zero shear stress and therefore maximum opening mode energy release rate and stress intensity factor. The hypothesis is that materials resist crack growth in shear and always turn to the direction that promotes mode I fracture.

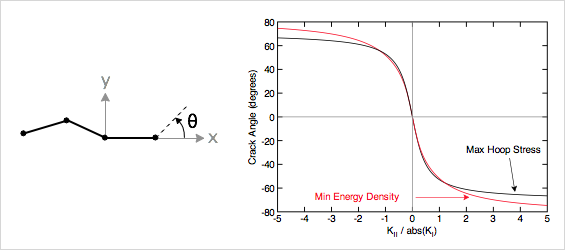
In this criterion, the crack direction is at angle θ (which is ccw from self similar growth, see figure below) and obeys

      [math]\displaystyle{ \cos\theta = {3R^2 + \sqrt{1+8R^2} \over 1+9R^2} \quad {\rm and} \quad \sin\theta = \mp\sqrt{1-\cos^2\theta} = - R(3\cos\theta - 1) }[/math]

where R = K_II/abs(K_I). In other words, the crack growth is along the vector (cos θ, sin θ) relative to the crack tip coordinate system. In the limit of K_I to zero, cos θ = 1/3 for crack direction of -70.5 (or +70.5) degrees. In the limit of K_II to zero, cos θ = 1 for crack direction 0 or self-similar crack propagation. This method requires K_I and K_II which can only be done for isotropic materials. For anisotropic materials, a variant the maximum hoop direction is the "cod hoop" method, which use the same approach except that R is calculated from R = δ_t/abs(δ_n). The following figure defines crack growth angle and plot that angle as a function of R.

Some papers implement maximum hoop direction using the equation

      [math]\displaystyle{ \tan {\theta\over 2} = {1\over 4}\left({1\over R} \mp \sqrt{{1\over R^2} + 8}\right) }[/math]

where the sign on the square root is determined by sign of K_II. This equation gives identical results to the equation above. Because the crack propagation only needs to know the normal vector (cos θ, sin θ), however, it is more efficient to evaluate them directly than to use one triginometric equation to find θ followed by more trigonometric functions to find the unit vector.

Minimum Strain Energy Density Direction

In the SED or minimum strain energy density model, the crack is postulated to grow in the direction where the strain energy density is a minimum. The crack direction depends on K_I and K_II (which means this method requires isotropic materials) and involves numerical solution to find θ The figure above plots the crack direction angle as a function of R (see red curve). The predictions are very similar to the maximum hoop stress direction.

Traction Law in Wake of Propagation

By default, cracks propagate as new, traction-free crack surfaces. Alternatively, the optional (tract) can define a material ID for a previously defined traction law material. When this parameter is used, new crack surfaces created by crack propagation will be initialized with the provided traction law material. To set (tract) without specifying a direction rule in (dir) in scripted files, set (dir) to the default value (or 0).

Note that crack surfaces cannot combine fraction and traction laws. Thus any crack that propagates into a traction law material must use a frictionless contact law. If any initial crack particles have a traction law material, the crack will automatically be converted to a frictionless contact crack. If the initial crack, however, has no traction laws, you must be sure to create that crack as a frictionless crack.

Crack Tip Materials

Many crack propagation properties are controlled by the properties of the crack tip material, such as K_Ic, K_IIc, J_Ic, initiation time, crack speed, etc.. These fracture toughness properties can be set for any material models. You must set all the ones needed by the selected propagation criterion.

When a simulation has more than one material, two new things happen. First, the simulation automatically tracks the crack tip material by evaluating the most prevalent material type near the crack tip. Second, you can customize all propagation properties for each material. In other words, the above Propagate command and optionally the AltPropagate descibed below, set the default propagation properties, but each material can use different settings if desired.

Two additional considerations about crack tip materials and crack propagation are:

1. The criteria "max energy release" (1), "elliptical" (5), and "energy density" (6) are based on stress intensity factors K_I and K_II. These factors can only be calculated for isotropic materials (which includes Isotropic, Mooney, HEIsotropic, Viscoelatic, and all their subclasses), which means only these material can use these criteria. Anisotropic materials are limited to criteria "steady state" (2), "max ctod" (6), and "critical err" (7). The "energy balance" (3) criteripn is not meant for general list.
2. Although you can model crack propagation in anisotropic materials, all fracture toughness properties are independent of crack orientation. In other words, all criteria are based on isotropic toughness properties (same toughness in all directions). The material may have anisotropic mechanical properties, but anisotropy in toughness is not yet modeled. See the alternate propagation criterion for one method to deal with anisotropic toughness properties.

Alternate Propagation Criterion

The AltPropagate command is used to define a competing crack propagation criteria within a single material. In scripted files, the command is

AltPropagate (crit),<(dir)>,<(traction)>

In XML files, the command, which must be in the <Cracks> block, is:

<AltPropagate criterion='(critNum)' direction='(dirNum)' traction='(traction)'/>

where (crit) and optionally (dir) and (tract) set alternate crack propagation using methods identical to setting the primary propagation properties except (crit) cannot be "steady state" (2) or "energy balance" (3).

The AltPropagate command lets you set a second propagation criterion to use in certain specific models that involve competing fracture modes. When an alternate criterion is used, the following steps take place:

1. At each time step, the first criterion is checked. If the situation is critical, the crack will propagate by the first criterion and the second criterion will subsequently be turned off for that crack tip.
2. As long as the first criterion has not become critical, the second or alternate criterion will be checked. The crack will propagate by that criterion if it is critical.
3. When propagation information is printed to the output file, it will include "(alt)" when propagating by the second criterion and will omit that wording once the primary criterion is activated.

This option is available to allow simulations of competing fracture modes such as crack growth along a weak interface vs. propagation away from the interface into the bulk material. For this problem, the first criterion is set to the bulk fracture properties and the second criterion is the interface fracture criterion. The later is usually set to be by self-similar crack growth or crack growth in the initial crack direction so it will be along the interface. In this scheme, the crack will propagate along the interface until turning into the bulk becomes critical. Once it turns into the bulk, the interface fracture mechanics is turned off.

The above commands set the default alternate crack propagation properties. In simulations with more than one material, you can set each material to use its own alternate propagation properties. By using only custom alternate propagation properties, some materials can have a single criteria while others have two criteria. The specific alternate propagation properties to use for any crack tip depend on the crack tip material.

Propagation Length

The PropagateLength command changes the amount of crack growth that occurs each time the crack propagates. In scripted files, the command is:

PropagateLength (relLength)

In XML files, the command is

<PropagateLength>(relLength)</PropagateLength>

where (relLength) is the amount of crack growth (entered as relative to cell dimensions) for each increment in crack growth.

When propagation is activated, the crack tip propagates whenever the current fracture criterion is reached. The PropagateLength command determines how far the crack propagates. The default setting is 0.5, or half an element per propagation increment. This setting often works well, but during impact conditions, it may not be enough. If the crack growth is too low, the critical conditions will still be exceeded and may actually grow beyond acceptable limits for the current material (e.g., J can greatly exceed J_c). Using a higher value can help such problems. It moves the current crack tip out of the current stress concentration and it waits there for stress to build up again resulting in more stable crack growth.

The physically correct increment is unknown, but it should not be so high as to cause artifacts or erratic crack growth. It should also not be so low as to numerically restrict crack speed. Since crack growth rate can reach wave speeds, the propagation length should never be lower than the Courant factor used to time step calculations). If propagation length is less than this value, it could never reach wave speed of the material, even if it propagates on every time step. A good check on influence of this setting is to vary its value and plot crack length vs. time. If the setting changes the crack propagation rates or makes crack growth erratic, its setting may be causing artifacts in the simulation.