Exponential Traction Law

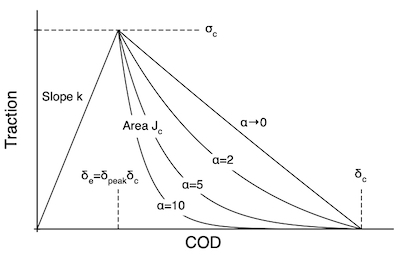
The Traction Law

This traction law assumes a linear elastic response up to σ_c followed by a scaled exponential decrease to reach zero at critical crack opening displacement (COD) of δ_c. The exponential decay in the post peak region (i.e., δ>δ_e) is given by

      [math]\displaystyle{ S(\delta) = \sigma_c\frac{e^{-\alpha\frac{\delta-\delta_e}{\delta_c-\delta_e}}-e^{-\alpha}}{1-e^{-\alpha}} }[/math]

This cohesive law defines traction as a function of crack opening displacement (COD) during uniaxial, monotonic loading. There are separate and uncoupled cohesive laws for opening displacement (mode I) and sliding displacement (mode II).

Notice how the shape changes with α. In the limit of α=0, this law is identical to the Triangular Traction Law (and that one should be used instead because it is more efficient. Increasing α causes traction to drop faster, which might simulate increasingly brittle response. The toughness of this cohesive law is the area under the curve that can be cast as

      [math]\displaystyle{ J_c = {1\over 2} \sigma_c\delta_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right) \quad{\rm where}\quad f(\alpha) = 2\left(\frac{1}{\alpha}-\frac{e^{-\alpha}}{1-e^{-\alpha}}\right) }[/math]

The function f(α) is 1 when α=0 and decays to zero as α increases. The toughness is thus bracketed by

      [math]\displaystyle{ {1\over 2} \sigma_c\delta_e \le J_c \le {1\over 2} \sigma_c\delta_c }[/math]

The minimum corresponds large α with an instant drop to zero traction at δ_e while the maximum corresponds to α=0 and is area under the corresponding Triangular Traction Law.

When creating this traction law, you have to enter α, exactly two of σ_c, δ_p, and k and either J_c or δ_c. These four required properties must be entered for both mode I and mode II. If you enter δ_c, then the missing one of σ_c, δ_p, and k are calculated from one of

      [math]\displaystyle{ k = {\sigma_c\over \delta_{peak}\delta_c} \qquad {\rm or} \qquad \delta_{peak} = {\sigma_c\over k\delta_c} \qquad {\rm or} \qquad \sigma_c = k \delta_{peak}\delta_c }[/math]

Finally J_c is found from the expression above. If instead you enter J_c, the calculation of δ_c depends on which two of σ_c, δ_p, and k are provided:

      [math]\displaystyle{ {\rm from\ }\sigma_c\ {\rm and}\ \delta_{peak}:\quad \delta_c = \frac{2J_c}{\sigma_c\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right)} }[/math]

      [math]\displaystyle{ {\rm from\ }\sigma_c\ {\rm and}\ k:\quad \delta_c = \frac{2kJ_c-\bigl(1-f(\alpha)\bigr)\sigma_c^2}{k\sigma_cf(\alpha)} }[/math]

      [math]\displaystyle{ {\rm from\ }\delta_{peak}\ {\rm and}\ k:\quad \delta_c = \sqrt{\frac{2J_c}{k\delta_p\left(\delta_{peak} + \bigl(1-\delta_{peak}\bigr)f(\alpha)\right)}} }[/math]

Once δ_c is found, the remaining property among σ_c, δ_p, and k is found using expression above.