Difference between revisions of "Double Exponential Softening"
| Line 44: | Line 44: | ||
</math> | </math> | ||
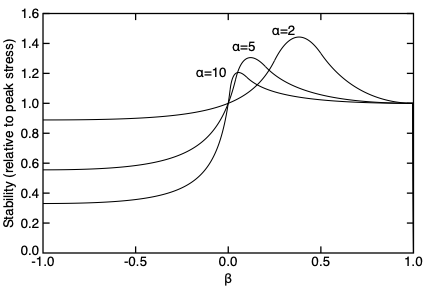
For <math>\beta=0</math>, the stability factor simplifies to <math>\eta = 1</math> which is identical to [[Exponential Softening]] (in fact the entire law is identical to [[Exponential Softening]] and that law should therefore be used instead). Although this stability factor goes to zero as <math>\beta\to1</math>, the ''effective'' stability is better compared to monotonically decreasing laws by | For <math>\beta=0</math>, the stability factor simplifies to <math>\eta = 1</math> which is identical to [[Exponential Softening]] (in fact the entire law is identical to [[Exponential Softening]] and that law should therefore be used instead). Although this stability factor goes to zero as <math>\beta\to1</math>, the ''effective'' stability is better compared to monotonically decreasing laws by multiplying <math>\eta</math> by its peak values squared (''i.e.'', minimum cell size is related to <math>\eta/\sigma_0^2</math> and <math>\sigma_0</math> decreases if set by reducing peak stress by <math>f_{peak}</math>). The figure on the right plots this ''effective'' stability factor as a function of <math>\beta</math> for various values of <math>\alpha</math>. Overall, the stability of this law is comparable to the stability of a single [[Exponential Softening]] law. | ||
== Softening Law Properties == | == Softening Law Properties == | ||
Revision as of 11:06, 20 July 2021
The Softening Law
The main goal of his softening law is to provide another softening law that can initiate at low stress, [math]\displaystyle{ \sigma_{0} }[/math] (from the damage initiation law), rise to a peak, [math]\displaystyle{ \sigma_0*f_{peak} }[/math], and then decay. With that goal in mind, the function is
[math]\displaystyle{ f(\delta,s) = \frac{1}{1-\beta}\left(e^{-k\delta} - \beta e^{-\alpha k\delta}\right) }[/math]
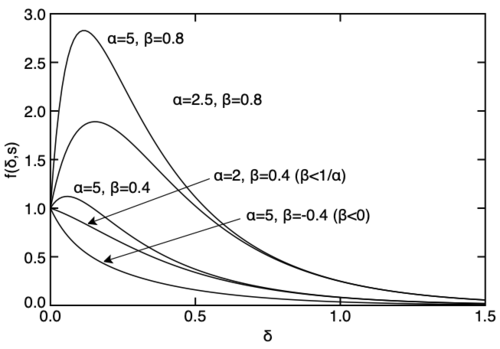
where [math]\displaystyle{ \alpha\gt 1 }[/math] (to have second term decay faster) and [math]\displaystyle{ \beta\lt 1 }[/math] (to keep [math]\displaystyle{ f(\delta,s)\gt 0 }[/math]). The figure on the right shows double exponential softening functions for various values of [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]. The law peaks whenever [math]\displaystyle{ 1/\alpha\lt \beta\lt 1 }[/math]. This behavior is valid for softening laws provided the modulus still monotonically softens (which is does for any valid parameters). The peak value of this function is located at:
[math]\displaystyle{ \delta_{peak} = \left\{ \begin{array}{ll} \frac{ \ln \alpha\beta }{k(\alpha-1)} & 1/\alpha\lt \beta\lt 1 \\ 0 & \beta \le 1/\alpha \end{array}\right. }[/math]
The corresponding peak value is:
[math]\displaystyle{ f_{peak} = \left\{ \begin{array}{ll} \frac{\alpha-1}{\alpha(1-\beta)(\alpha\beta)^{\frac{1}{\alpha-1}}} & 1/\alpha\lt \beta\lt 1 \\ 1 & \beta \le 1/\alpha \end{array}\right. }[/math]
When using this law, you enter the initiation stress into the initiation law. If you want to set the peak stress instead, the initiation stress should be reduced from that peak stress by this value of [math]\displaystyle{ f_{peak} }[/math]. When [math]\displaystyle{ \beta\lt 1/\alpha }[/math], this law monotonically decreases from 1 to 0. For [math]\displaystyle{ \beta\lt 0 }[/math], this law is a simple double-exponential decay function.
The value for [math]\displaystyle{ k }[/math] is is found from
[math]\displaystyle{ sG_c = \int_0^{\infty} f(\delta,s) = \frac{\alpha-\beta}{k\alpha(1-\beta)s} \quad{\rm or}\quad k = \frac{\alpha-\beta}{\alpha(1-\beta)sG_c} }[/math]
Here s is the softening scaling term and Gc is toughness of the law. The decay rate, [math]\displaystyle{ k }[/math], which depends on mesh size and crack orientation, is calculated from s and Gc and is not a law property to be provided.
The stability factor depends on relative values of [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]:
[math]\displaystyle{ \eta = \left\{ \begin{array}{ll} \frac{\alpha^2(1-\beta)^2(\alpha^2\beta)^{\frac{1}{\alpha-1}}}{(\alpha-\beta)(\alpha-1)} & {\rm for\ } \beta\gt 1/\alpha^2 \\ \frac{\alpha(1-\beta)^2}{(\alpha-\beta)(1-\alpha\beta)} & {\rm for\ } \beta \lt 1/\alpha^2 \end{array}\right. }[/math]
For [math]\displaystyle{ \beta=0 }[/math], the stability factor simplifies to [math]\displaystyle{ \eta = 1 }[/math] which is identical to Exponential Softening (in fact the entire law is identical to Exponential Softening and that law should therefore be used instead). Although this stability factor goes to zero as [math]\displaystyle{ \beta\to1 }[/math], the effective stability is better compared to monotonically decreasing laws by multiplying [math]\displaystyle{ \eta }[/math] by its peak values squared (i.e., minimum cell size is related to [math]\displaystyle{ \eta/\sigma_0^2 }[/math] and [math]\displaystyle{ \sigma_0 }[/math] decreases if set by reducing peak stress by [math]\displaystyle{ f_{peak} }[/math]). The figure on the right plots this effective stability factor as a function of [math]\displaystyle{ \beta }[/math] for various values of [math]\displaystyle{ \alpha }[/math]. Overall, the stability of this law is comparable to the stability of a single Exponential Softening law.
Softening Law Properties
Only one property is needed to define a cubic step function softening law:
| Property | Description | Units | Default |
|---|---|---|---|
| Gc | The toughness associated with the this softening law | energy release units | none |
| k | Initial slope of the law (must be nonnegative) (OSParticulas only) | none | 0 |