Surface Normals

Both multimaterial mode MPM and explicit cracks need to calculate surface normals. These normals are a crucial step in accurate contact physics calculations.

Introduction

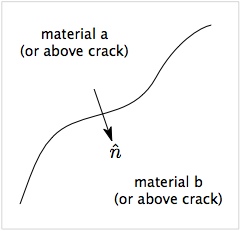
The figure shows a surface between two materials (a and b) or between two sides of a crack (above and below). The arrow shows a vector normal to the surface oriented from side a to side b. Finding this normal accurately is a key component of implementing both multimaterial mode contact and crack contact. First, normals are needed to find the component of the velocity in the approaching direction and the separation in the opneing direction, both of which are used to detect contact. Second, the normals are needed to implement contact mechanics such as to model frictional contact or imperfect interfaces.

Practical experience using multimaterial mode MPM simulations has revealed that accuracy of results is very sensitive to the method used to find the normals. In fact, when a multimaterial mode simulation has numerical issues, the causes of those issues is almost always connected to problems in finding surface normals. See below for the various options in multimaterial mode MPM to finding normals. Numerous options are needed because no on option works for all problems.

Simulations that use explicit cracks, have far fewer issues with normals. The normals are still crucial, but because the crack geometry is tracked, the crack normals are more easily calculated. See below for some details on crack surface normals.

Multimaterial Normal Vector Options

NairnMPM has implemented several methods for finding normals in multimaterial mode contact. No one method works for all problems, which is why multiple options are needed. This section describes the available options.

Each Material's Gradient

When multimaterial mode MPM was initially developed, contact was handled separately for each material's velocity field and the normal vector was found from that material's mass gradient.. The alorithm is straightforward and is extended to more than two materials in contact simply for iterating for each material. Experience shows it suffers in accuracy compared to methods desribed below. For one thing, the normals for the two materials when generally not be in equal and opposite directions. When that occurs, the contact algorithm does not conserve momentum.

This method is selected by setting (normals) to owngrad (or numerically to 3). This option is available in NairnMPM for comparison to improved methods and not recommended for general use.

Average Gradient

This method (and other improvements below) are described in more detail in Nairn (2013).. The first obvious improvement to conserve momentum is to find the average mass gradient between the two materials and use that normal for both sides of the crack. If the multimaterial mode has [[Multimaterial MPM#More than Two Materials|more than two materials, the average is found between one material and the remaining materials lumped into a virtual material.

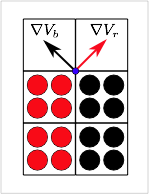
This method can also improve calculations at edge nodes. The figure on the right shows two materials in contact at the edge of an object. The mass gradients for the red and black materials are shown by the vectors. Both of these normal are inaccurate for the contacting surfaces, but averaging the normals (with correct signs, gives normal vector in the horizontal direction that exactly matches the contact surface normal.

This method is selected by setting (normals) to avggrad (or numerically to 2).

Maximum Gradient

This method is selected by setting (normals) to maxgrad (or numerically to 0).

Maximum Volume

This method is selected by setting (normals) to maxvol (or numerically to 1).

Custom Specified Normal

Developer flags and maybe more options int he future

Explicit Crack Normal Vector

Found from crack path and often more accurate the multimaterial mode such as for interfaces.