Crack Settings
These command control modeling of explicit cracks and whether or not those cracks propagate
Introduction
The extension of MPM to model explicit cracks is called CRAMP for CRAcks in the Material Point Method. It is described first in a paper by Nairn (2003).[1]. Some other papers discuss calculation of J integral and stress intensity factor,[2], propose energy balance propagation,[3] handle cracks in 3D (although not currently available in NairnMPM,[4], use cracks to model imperfect interfaces,[5], and use traction laws with cracks.[6] Some applications of using cracks in MPM include wood fracture,[7] use of cracks to model glue bods in oriented strand board,[8] simulation of dynamic fracture,[9] and simulation of crack growth with fiber bridging.[10]
The commands is this section are used to set various features of the crack physics and crack propagation for any explicit cracks in the object.
Crack Settings Commands
In scripted files, crack properties are controlled by these possible commands
(Crack Propagation Commands) Friction Imperfect Interface JContour (size),(terms) ContactPosition MovePlane
In XML input file, all global crack setting commands are within a <Cracks> element that must be within the <MPMHeader>:
<Cracks> (Crack Propagation Commands) <Friction>0.3</Friction> <JContour size="(size)" terms="(terms)"/> <ContactPosition>0.8</ContactPosition> <MovePlane type='avg' prevent='no'/> </Cracks>
The Crack Propagation Commands are described in a separate help top. The other commands are describe in the following sections.
Crack Contact Properties
J Integral Contour Settings
The JContour command is used to set the size of the path used for evaluating J integral and and control the number of terms used in the process. The details are:
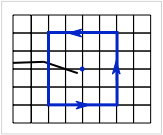
- (size) - the J integral is evaluated on a rectangular contour center on the grid node closet to the crack tip (see blue line in the figure). The (size) setting is the semi-length for the sides of the rectangle. The default value is 2 (as shown in the figure).
- (terms) - this optional parameter should be set to 1 or 2 to specify if the J Integral should be a simple contour (1) or include an area integral inside the contour (2). The area integral corrects for dynamic effects and for axisymmetric stress states making the calculation path independent even in dynamic problems, but is slower. A contour alone (1) might be enough if the size of the contour is small (e.g., (size)=2) and the loading is slow, but both contour and area might be essential as the problem becomes more dynamic or as the size of the contour grows. The default is 1, but for axisymmetric calculations, the area integral is needed even for static problems, and therefore the default changes to 2 terms.
More details on J integral evaluation and on the two J integral terms are given in Guo and Nairn (2006).[2]
Crack ContactPosition Command
This command influences the way crack detect contact between the crack surfaces. Its function and use is described here.
Crack Plane Updating
The MovePlane command determines how a crack plane move and whether or not crack surfaces can cross crack planes. In scripted files, the command is
MovePlane (method),<(prevent)>
In XML files, the command is:
<MovePlane type='(method)' prevent='(prevent)'/>
where
- (method) is 'avg' to move the crack plane to the midpoint of the top and bottom surfaces or 'cm' to move the crack plane in the center of mass velocity field. The default method is 'avg'.
- (prevent) is 'yes' or 'no' to prevent or allow crack planes crossing the main crack plane. The default setting is 'no'.
For all cracks, the top and bottom surfaces move in their separate velocity fields. The setting for (method) determines only how the crack plane particles move. The two methods are equivalent for well defined cracks, but may give different results is some problems. Thus, if crack position seems to cause a problem, one possibility is to repeat the analysis with the other (method) option.
Similarly, both (prevent) settings are equivalent for well behaved cracks (because surfaces of such cracks tend to not pass through crack planes). If a simulation has problems tracking surfaces, you can try setting (prevent) to 'yes' to see how it changes. The 'no' setting is faster because it does not need to check crack surfaces on each time step.
References
- ↑ J. A. Nairn, "Material Point Method Calculations with Explicit Cracks," Computer Modeling in Engineering & Sciences, 4, 649-664 (2003). (See PDF)
- ↑ 2.0 2.1 Y. Guo and J. A. Nairn, "Calculation of J-Integral and Stress Intensity Factors using the Material Point Method," Computer Modeling in Engineering & Sciences, 6, 295-308 (2004). (See PDF)
- ↑ J. A. Nairn, "Simulation of Crack Growth in Ductile Materials,"; Engr. Fract. Mech., 72, 961-979 (2005). (See PDF)
- ↑ Y. Guo and J. A. Nairn, "Three-Dimensional Dynamic Fracture Analysis Using the Material Point Method," Computer Modeling in Eng. & Sci., 16, 141-156 (2006). (See PDF)
- ↑ J. A. Nairn, "Numerical Implementation of Imperfect Interfaces, Computational Materials Science, 40, 525-536 (2007). (See PDF)
- ↑ J. A. Nairn, "Analytical and Numerical Modeling of R Curves for Cracks with Bridging Zones," Int. J. Fracture, 155, 167-181 (2009). (See PDF)
- ↑ J. A. Nairn, "Material Point Method Simulations of Transverse Fracture in Wood with Realistic Morphologies," Holzforschung, 61, 375-381 (2007). (See PDF)
- ↑ J. A. Nairn and E. Le, "Numerical Modeling and Experiments on the Role of Strand-to-Strand Interface Quality on the Properties of Oriented Strand Board," Proc of 9th Int. Conf. on Wood Adhesives, Lake Tahoe, Neveda, USA, Sept. 28-30, 2009. (See PDF)
- ↑ S. G. Bardenhagen, J.A. Nairn, and H. Lu, "Simulation of dynamic fracture with the Material Point Method using a mixed J-integral and cohesive law approach," Int. J. Fracture, 170, 49-66 (2011).
- ↑ N. Matsumoto and J.A. Nairn, "Fracture Toughness of Wood and Wood Composites During Crack Propagation," Wood and Fiber Science, in press (2012). (See PDF)