Cubic Traction Law

The Traction Law

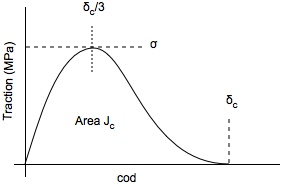
This traction law assumes use a cubic function for traction as a function of crack opending displacement (COD). This cubic relation is choosen such that the slope is zero at δ_c and the peak always occurs at δ_c. This traction law was first proposed by Needleman. It has a convenient smooth shape for numerical calculations and the zero slope at δ_c may be desirable. There is no physical basis to claim it is more realistic than other traction laws. The resulting function is

      [math]\displaystyle{ \sigma = {27\over 4}\sigma_{max} {\delta\over\delta_c}\left(1-{\delta\over\delta_c}\right)^2 }[/math]

There are separate traction laws for opening displacement (mode I) and sliding displacement (mode II).

The toughness of this traction law is the area under the curve or:

      [math]\displaystyle{ J_c = {9\over 16} \sigma\delta_c }[/math]

When creating this traction law, you have to enter exactly two of these failure properties for both mode I and mode II (i.e., two of J_Ic, σ_I, and δ_Ic and two of J_IIc, σ_II, and δ_IIc). Whichever property is not specified will be calculated from the two provided properties using one of the following relations:

      [math]\displaystyle{ \delta_c = {16J_c\over 9000\sigma}, \qquad \sigma = {16J_c\over 9000\delta_c}, \qquad {\rm or} \qquad J_c = {\over 16}\sigma\delta_c }[/math]

These relations assume J_Ic in J/m², σ in MPa, and δ_c in mm.

Traction Law Properties

The following properties are used to create a triangular traction law:

Property	Description	Units	Default
(other)	Properties common to all traction laws	varies	varies