Triangular Traction Law

Traction Law

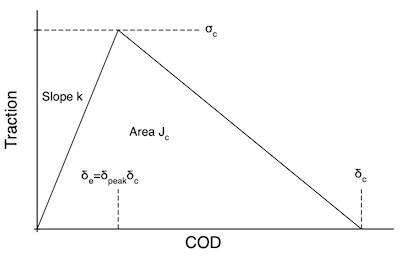
The traction laws in pure mode I or pure mode II each have the triangular shape shown in the figure. There are separate traction laws for opening displacement (mode I) and sliding displacement (mode II).

The toughness of this traction law is the area under the curve or:

      [math]\displaystyle{ J_c = {1\over 2} \sigma\delta_c }[/math]

When creating this traction law, you have to enter exactly two of these failure properties for both mode and mode II (i.e., two of J_Ic, σ_I, and δ_Ic and two of J_IIc, σ_II, and δ_IIc). Whichever property is not specified will be calculated from the other properties using the following relations:

      [math]\displaystyle{ \delta_c = {J_c\over 500\sigma}, \qquad \sigma = {J_c\over 500\delta_c}, \qquad {\rm or} \qquad J_c = 500\sigma\delta_c }[/math]

These relations assume J_Ic in J/m^{2, σ in MPa, and δ_c in mm.}

To get the initial rise of the curve, you must zero slope, k, and crack opening displacement You must enter zero or one of the terms above for each mode (i.e., zero or one of kIe and delpkI and zero or one of kIIe and delpkII). If one is provided, the other will be calculated from k = σ/(δpeak δc). A valid traction law requires δpeak ≤ 1. If neither k nor δpeak are entered, the peak will be located at δpeak = 0.225926299. This location provides the closest match to the cubic traction law for area under the curve as a function of δ. The initial slope will be set to k = σ/(0.225926299 δc).