Defining Cracks

This section explains how to add explicit cracks to an MPM simulation.

Introduction

The extension of MPM to model explicit cracks is called CRAMP for CRAcks in the Material Point Method. The commands is this section are used to define the explicit cracks (and there can be any number of them). In addition, whenever a simulation has cracks you can use crack settings commands to customize the features of the crack physics and set various material fracture properties to control crack propagation.

The development of CRAMP is described first in a paper by Nairn (2003) (and its development was done using NairnMPM). Some other papers discuss calculation of J integral and stress intensity factor,, propose energy balance propagation, handle cracks in 3D (although not currently available in NairnMPM), use cracks to model imperfect interfaces,, and use traction laws with cracks. Some applications of using cracks in MPM include wood fracture, use of cracks to model glue bonds in oriented strand board, simulation of dynamic fracture, and simulation of crack growth with fiber bridging.

Crack Definition Commmands

In CRAMP, a crack is defined as series of massless particles connected by crack segments. The first particle is the "start" tip and the last particle is the "end" tip. When CRAMP is active, nodes around the crack will be divided into two velocity fields to separately model motion of particle "above" the crack and "below" the crack. You define a crack by providing the points along the crack - (x₁,y₁) to (x_n,y_n). In addition, CRAMP fully accounts for crack contact, can model cracks with frictional contact, can use cracks to model imperfect interfaces, and can insert traction laws to model cohesive zones. When defining cracks, some additional commands are available to set crack contact mechanics, set crack tip materials, and insert traction laws.

In scripted files, a single crack is started with a NewCrack command, which is followed by one or more of the other commands to complete the crack definition:

NewCrack (x1),(y1),<(mat)>,<(frict)>,<(tract)>
GrowCrack (x2),(y2),<(mat)>,<(tract)>
GrowCrackLine (x2),(y2),(segs),<(mat)>,<(tract)>
GrowCrackArc (x1),(y1),(x2),(y2),(segs),(ang1),(ang2),<(mat)>,<(tract)>
CrackInterface (Dt),(Dntens),(Dncomp)
CrackThickness (thick)

In XML files, each crack is defined in a <CrackList> element:

<CrackList friction='(frict)'>
  <pt units='mm' x='(x1)' y='(x2)' tip='(mat)'/>
  <pt x='53' y='0'/>
     . . .
  <pt x='(x2)' y='(y2)'/>
  <Line xmin="(x1)" ymin="(y1)" xmax="(x2)" ymax="(y2)" resolution="(segs)"
           start_tip="(mat)" end_tip="(mat)"/>
  <Circle xmin="(x1)" ymin="(y1)" xmax="(x2)" ymax="(y2)" resolution="(segs)"
           start_tip="(mat)" end_tip="(mat)" start_angle="(ang1)" end_angle="(ang2)"/>
  <Thickness>(thick)</Thickness>
</CrackList>

The commands and their functions are:

• NewCrack command - this command starts a new crack (in XML files, the <CrackList> element and its first geometry command starts the crack).
• GrowCrack, GrowCrackLine, and GrowCrackArc commands - these commands extend the crack (the corresponding XML commands are <pt>, <Line>, and <Circle>).
• CrackInterface command - this commands set the crack to be an imperfect interface.
• CrackThickness command - this commands sets the crack thickness (the corresponding XML command is <Thickness>).

Starting the Crack

In scripted files, a crack is started with the NewCrack command:

NewCrack (x1),(y1),<(mat)>,<(frict)>,<(tract)>

In XML files, a crack is started with

<CrackList friction='(frict)'>
  <pt units='mm' x='(x1)' y='(x2)' tip='(mat)'/>

where

• (x1),(y1) - defines the coordinates for the start tip of the crack (the coordinates are (R,Z) if axisymmetric).
• (mat) - this optional parameter can be one of three things:
  1. A Material ID - It can define the material at the start of the crack. Crack propagation is only possible when one or both of its crack tips have a material ID. If the material ID is omitted, the MPM calculations will correctly model that crack, but no propagation or fracture parameter calculations will occur. In XML files, this (mat) option must set the material by number.
  2. "exterior" - this text indicates a crack tip at the edge of the body. In XML files, use tip='-2' instead of of the word "exterior".
  3. "fixed" - this text indicates a fixed crack (scripted files only). A fixed crack will not translate with the object and will not track surfaces. It can calculate J Integral but not stress intensity factor. It is useful when using cracks to create surfaces in an object. The surface can change by propagating the crack at constant crack speed initiated by critical J or by initiation time (see steady state propagation). In XML files, you set a "fixed" crack, by adding an attribute type='fixed' to the <CrackList> element rather then using the (mat) parameter.
• (frict) - the global Friction command sets cracks by default to contact by frictional sliding and selects default frictional properties. By using the (frict) parameter, you can customize any specific crack to use different frictional properties on can convert one crack to use frictional sliding when the default crack setting is to model imperfect interfaces. The custom frictional properties are set using the same options available in the Friction and FrictionMM commands. If you want to set a contact law on a non-fixed crack in scripted files, but do not want to define a tip material in (mat), you can enter (mat)="free", and then enter the desired (frict).
• (frict) and (tract) - alternatively, these optional parameters can assign a traction law to the initial crack tip. To use this option in scripted files, set (frict)="traction" and then set (tract) to a material ID for a traction law material. The traction law will be applied only to the first crack particle. In XML files, you assign a traction law using a mat='n' or matnam='name' attribute on the <pt> command. (See notes 3 and 4).

Growing the Crack

Once a crack is started, it is extended by using one or more growing commands. In scripted files, the commands are:

GrowCrack (x2),(y2),<(mat)>,<(tract)>
GrowCrackLine (x2),(y2),(segs),<(mat)>,<(tract)>
GrowCrackArc (x1),(y1),(x2),(y2),(segs),(ang1),(ang2),<(mat)>,<(tract)>

In XML files, the growing commands are:

  <pt x='(x2)' y='(y2)' tip='(mat)' mat='(tract)'/>
  <Line xmin="(x1)" ymin="(y1)" xmax="(x2)" ymax="(y2)" resolution="(segs)"
           start_tip="(mat)" end_tip="(mat)" mat='(tract)'/>
  <Circle xmin="(x1)" ymin="(y1)" xmax="(x2)" ymax="(y2)" resolution="(segs)"
           start_tip="(mat)" end_tip="(mat)" start_angle="(ang1)"
           end_angle="(ang2)" mat='(tract)'/>

• (x1,y1) and (x2,y2) define two points that are used in the growing action that results from the command (the coordinates are (R,Z) if axisymmetric). Some commands give only (x2,y2); for these commands (x1,y1) is the given by the last point of the previous crack definition command.
• (segs) - the number of segments to create in the command's growing action. See note on number of segments for recommendations in selecting this number.
• (ang1) and (ang2) - for the arc commands, these parameters define the start and end angles for the arc growing action.
• (mat) - this optional parameter can be one of two things:
  1. A Material ID - it can define the material at the end of the growing action. Crack propagation is only possible when one or both of its crack tips have a material ID. If the material ID is omitted, the MPM calculations will correctly model that crack, but no propagation or fracture parameter calculations will occur. A crack tip material is only needed if the growing command is the last crack definition command for the current crack. In XML files, this (mat) option must set the material by number and if desired you set a material for both the first and last particle generated by the command.
  2. "exterior" - this text indicates a crack tip at the edge of the body. In XML files, use tip='-2' instead of of the word "exterior" and it can set either the first or last particle generated by the command. A setting of "exterior" only has an effect if the growing command is creating the tip particles for the crack.
• (tract) - this optional parameter can assign a traction law to all new crack particles created by the growing action by setting it to the material ID for a traction law material. To set a traction law material but no crack tip material in (mat) in scripted files, you can set(mat) to "0" (or actually to any invalid material ID). In XML files, you assign a traction law using a mat='n' or matnam='name' attribute on the command. (See notes 3 and 4).

The growing actions for the various crack definition commands are:

• GrowCrack and <pt> - create a single crack particle at (x2,y2) and one crack segment from (x1,y1) to (x2,y2).
• GrowCrackLine and <Line> - create (segs) crack particles and segments evenly spaced along the line from (x1,y1) to (x2,y2).
• GrowCrackArc and <Circle> - the points (x1,y1) define (x2,y2) are used to define the corners of a rectangle and an arc is followed between the two (ang1) and (ang2) angles (in degrees as counter-clockwise angles from the positive x axis). The arc is divided into (segs) evenly spaced particles and segments. In addition, the last point of the previous crack definition command will be connected with one segment to the start of the arc. Because the control points for the arc are the boundaries of the oval's rectangle and not the starting and ending points of the resulting arc, linking arcs with points and lines may cause jumps in the crack geometry. One solution is to choose the previous crack definition command to end at the resulting starting point of the arc.

Crack as Imperfect Interface

The global ImperfectInterface command sets cracks by default to be an imperfect interface and selects default interface parameters. By using the CrackInterface command, you can customize any specific crack to use different interface parameters. This command can also convert one crack to be an imperfect interface when the default crack setting is for frictional sliding. In scripted files, you can customize the current crack with:

CrackInterface (Dt),(Dntens),<(Dncomp)>

In XML files, you select an imperfect interface using attributes on the <CrackList> element

<CrackList Dt='(Dt)' Dn='(Dntens)' Dnc='(Dncomp)'>

where (Dt),(Dntens),(Dncomp) are the interfacial stiffness parameters and should be entered with units of MPa/mm. See imperfect interfaces documentation for details on modeling with interface and for information on setting the three interface parameters.

Crack Thickness

The CrackThickness command sets the thickness for an explicit crack. It is only needed if the crack has any particles with a traction law or when crack tips release their energy into heat. In the scripted file, the command is

CrackThickness (thick)

and it applies to the current crack started with the most recent NewCrack command. In XML files, the command, which must by within a <CrackList> element, is:

<Thickness>(thick)</Thickness>

where (thick) is the crack thickness (in mm).

Once a CrackThickness command has been used, all subsequent cracks will use the same thickness unless a new CrackThickness command changes it. If the grid was created using a GridThickness command (or a thickness attribute), the crack thickness will inherit that thickness. You only need a CrackThickness command to have a different thickness (although having a different thickness is very uncommon and may alter the physics of the cracks.)

Interacting Cracks

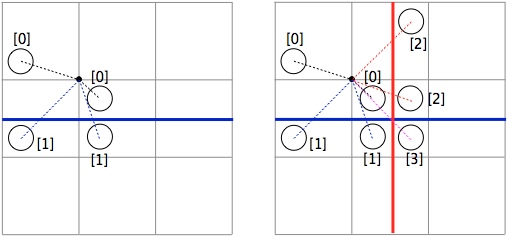
The key change in CRAMP compared to conventional MPM is that each node can have more then one velocity field to separately track particle motion above and below cracks. When only a single crack is near a node, that node may have velocity fields. When MPM extrapolates particle velocities to the grid, it traces a line from each particle to the node. If the line does not cross any crack, it adds to velocity field [0] on that node. If it crosses the single crack, it adds to velocity field [1]. The left side of the figure on the right show a single blue crack. The particles labeled [0] are on the same side of the crack as the indicated node and extrapolate to velocity field [0] on that node. The particles labeled [1] are on the opposite of the crack and extrapolate to velocity field [1] on that node.

The right side of the figure shows extension of CRAMP to handle two interacting cracks. When two cracks are near a node, that node may have up to four velocity fields, which are determined by tracing lines from particles to the node. Field [0] is from particles on the same side of both cracks. Field [1] is from particles on the opposite side of the first crack (here the blue crack). Field [2] is from particles on the opposite side of the second crack (the red crack). Field [3] is from particles that are on the opposite side of both cracks.

The extension to three interacting and explicit cracks is not handled. In other words, MPM models cannot explicitly resolve three cracks that are all near a single node (i.e., within the same background cell). If three crack are found, the simulation will continue and a warning will appear in the output file. The results near those three interacting cracks may not be accurate. Note that although three cracks in the same cell are not handled, an MPM model can handle any number of cracks as long as no more then two are near any given node. Despite this limitation, CRAMP does handle two cracks in the same cell, which is an improvement over typical finite element methods (e.g., XFEM) that are limited to just a single crack in any element.

Before CRAMP, some particle-based methods proposed to handle cracks with a simpler "node visibility" approach. The main difference is that these earlier methods use only a single velocity field on each node. During extrapolations, they use a similar ray-tracing method, but when the line crosses a crack, the information from that particle is ignored. In CRAMP, no information is ignored and both velocity fields are tracked using all available information. The use of multiple velocity fields also allows CRAMP to track motion of crack surfaces that can be used to track crack opening displacements, implement fracture mechanics methods, and allow for cohesive laws on cracks.

Exterior Cracks

For cracks that extend outside the object, the recommended approach is to stop the cracking slightly before the edge (e.g., 1/4 to 1/2 a cell from the edge) and define that tip as an "exterior" crack tip. Such tips are virtually extended beyond the object during calculations to model a crack through to the object's edge. An alternative is simply run the crack beyond the edge (e.g., 1/2 to 1 cell beyond the edge). Such crack tips, however, can suffer inaccuracies due to lack of information about local velocity fields. The result is such crack tips may not move correctly if the object is moving. Using an "exterior" crack tip resolves this problem.

Notes

1. Although a straight crack can be mathematically defined with a single segment, the crack surfaces and plane of such cracks would not update well under arbitrary deformation states. Instead cracks should be defined with at least one segment per cell of the background grid. If the crack has traction laws, experience suggest the crack should have at least two segments per cell.
2. For cracks with traction laws, the crack contact mechanics handles normal stresses for the case where the crack surfaces are in contact. To avoid invalid tangential force due to contact friction when cracks are in contact, any crack surface with traction laws will automatically convert to a frictionless crack regardless of settings you use for the crack's contact condition. If, however, you use propagation methods that assign traction laws to new crack surfaces, that crack may not automatically convert to a frictionless crack. You must therefore set such cracks to use frictionless crack contact.
3. For planar 2D calculations cracks that have traction laws must have the correct crack thickness.