Detecting Contact

Both multimaterial mode MPM and explicit cracks need to detect when two surfaces are in contact. This page describes the contact detection options.

Basic Contact Detection

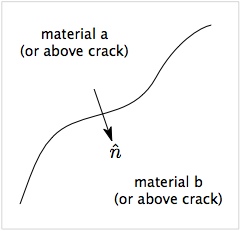
The figure shows a surface between two materials (a and b) or between two sides of a crack (above and below). The arrow shows a vector normal to the surface oriented from side a to side b. For both multimaterial contact and crack contact, the first step is to decide if the two velocity fields at the node are actually in contact. NairnMPM uses two criteria to detect contact.

Approach velocity

The first step is to decide if the two surface are approaching each other in the normal direction. This criterion reduces to       [math]\displaystyle{ \Delta\vec v \cdot \hat n \lt 0 \qquad {\rm where} \qquad \Delta\vec v = \vec v_a - \vec v_b }[/math] When this criterion is not satisfied, the surfaces are separating and assumed to not be in contact. In early multimaterial MPM, this criterion alone was assumed sufficient to be in contact. It is easy to visualize, however, that this assumption detects contact when surfaces are approaching each other but are still separated. For improved contact, a second criterion based on displacements is added.

Displacement check

If the approach velocity criterion is satisfied, NairnMPM next looks at displacements or positions of the two velocity fields. Basically, this criterion calculates the location of the two surfaces. If they overlap in the normal direction the surfaces are in contact. If they are separated, the surfaces are not in contact. Two ways to find contact surfaces by their surface location are to extrapolate particle displacements or particle positions. These methods are described in the section on the ContactPosition command.

Both multimaterial mode contact and crack contact use the above two criteria. Note that an accurate normal vector is crucial to contact detection and contact physics.

Explicit Crack Contact Detection

The only option you can change for crack contact detection is the method to calculate crack surface positions. The details are described in the following section on the ContactPosition command.

ContactPosition Command

When evaluating the displacement check to detect contact, the code extrapolates particle positions within each velocity. The opening displacement normal to the surfaces is found from

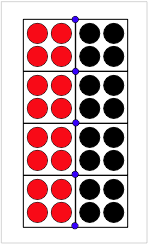
      [math]\displaystyle{ \delta_n = (\vec x_b-\vec x_a)\cdot\hat n }[/math]

where x_a and x_b are the extrapolated positions for material above and below the surface and n is the surface normal. But, inherent imprecision of surfaces in MPM (or any particle method) causes a problem. Consider the two surfaces in the figure on the right. When calculations start, their nodal positions extrapolated to common nodes (the blue nodes) will show a positive separation. Calculations with MPM shape functions with two particles per cell in each direction show that the calculated separation based on positions of two surfaces precisely in contact is

      [math]\displaystyle{ \delta_n \approx 0.8\Delta x }[/math]

where Δx is the cell dimension along the contacting axis. In other words, a contact criterion of δ_n<0 for contact would not detect contact correctly.

Three approaches can resolve this issue:

1. Extrapolate particle displacements instead of particle positions to the velocity fields. Now the separation for two surfaces in contact when calculations start is zero and a subsequent finding of δ_n<0 will indicate contact.
2. Define a contact-position offset, such as δ_con= 0.8δx and detect contact when δ_n<δ_con.
3. Undertake of more precise analysis of relation between extrapolated position of a material and actual distance to a node. First, we write the separation as:
   
         [math]\displaystyle{ \delta_n = d(d_{b,ext})-d(d_{a,ext}) \quad {\rm where} \quad d(d_{m,ext}) = (\vec x_m-\vec x_i)\cdot\hat n }[/math]
   
   where [math]\displaystyle{ d(d_{m,ext}) }[/math] is a function that finds actual distance to a nearby node as a function of the apparent or extrapolated distance. Calculations with MPM shape functions with two particles per cell in each direction led to the following function to convert extrapolation distance to actual distance:
   
         [math]\displaystyle{ {d(d_{ext})\over\Delta x} = \left\{\begin{array}{ll} 1-2\left({-d_{ext}\over 1.25}\right)^{0.58} & d_{ext}\lt 0 \\ 2\left({d_{ext}\over 1.25}\right)^{0.58}-1 & d_{ext}\gt 0 \end{array}\right. }[/math]
   
   Contact occurs when [math]\displaystyle{ \delta_n\le0 }[/math]

All three options are available in NairnMPM. The first (or displacements) method requires all contact situations to exist in the initial state. This situation is common in crack or interface modeling. The second and third methods must be used when these requirements are not met, which is true for any problem where surfaces start out apart and then move into contact during the simulation.

The use of displacements or positions can be set independently for multimaterial contact and crack contact. For multimaterial calculations, pick the desired option using the ContactPosition command. For crack contact, pick the desired option using the ContactPositionCrack command. Multimaterial mode contact most commonly uses the correctly position method (with a ContactPosition command) while crack modeling most commonly uses the displacement command (with no ContactPositionCracks command). For backward compatibility when separate settings were not allowed, simulations run in single material mode with cracks, will treat a ContactPosition command as a synonym for a ContactPositionCrack command.

For cracks, the most common approach is to use displacements instead of position with an offset, but cracks that model dynamic interfacial contact might need to switch to a position method instead. One example of this use in cracks is found in a paper on using cracks to model glue bond lines in oriented strand board.

For imperfect interface modeling with cracks or in multimaterial mode, you must use the displacements method whenever the interface law has non-zero tangential traction. The reason is that it is not possible to determine tangential displacement dicontinuity from extrapolated positions. When you must use displacements, the imperfect interfaces must all be in contact in the initial state. This requirement is normally not an issue because interface modeling usually involves interfaces that can be modeled as starting in contact. One issue is if you want to model both dynamic contact that needs position extrapolation along with interfaces that need displacement extrapolation. This type of simulation currently cannot be done, but an alternative is to model the interfaces using a crack with a traction law (although traction laws work with position extrapolations, they are not as accurate as when using extrapolated displacements).

Selecting ContactPosition Options

By default, NairnMPM extrapolates particle displacements to velocity fields and uses relative displacements of the two surfaces to detect contact. To switch to extrapolating particle positions instead and pick a method for converting positions into surface separation, scripted files can add the command:

ContactPosition (cutoff)

and XML files, the command to add is

<ContactPosition>(cutoff)</ContactPosition>

which can be in either the multimaterial block or the explicit cracks block of the <MPMHeader>. In both commands, the value entered for (cutoff) determines the method used:

• (cutoff)> 0: A positive value means to subtract (cutoff) from apparent separation to find actual separation (see method 2 in previous section). When using this method and two particles per cell, the (cutoff) should always be 0.8. If it is decreased, surfaces will visually come into contact before the particles reach each other. If it is larger than 0.8, objects will visually interpenetrate each other before contact is activated. This universal number was determined by MPM shape function calculations.
• (cutoff)< 0: A negative values means to use a function to determine actual separation. The function that is used is given in method 3 in the previous section. The absolute value of the entered parameter is used as the exponent in that power-law expression. With two particle per cell, this number should always be -0.58 (i.e., exponent wiill be 0.58).

Note that setting (cutoff)=0 is not the same as omitting the command. It will use method 2 in previous section with zero subtraction and result in detecting contact before particles actually reach contact.

Notes

1. Note that the universal values of 0.8 and -0.58 apply only to calculations with two particle per cell in each direction. The positive cutoff has to be changed for other particle sizes. For one particle per cell, a good value is 1.07. For three or more particle per cell, the value can be varied until get good visual results in simple contact. The value should decrease as the number of particles per cell increases. A negative cutoff corresponds to a specific function that applies only when two particle per cell in each direction. Use of any other number of particles should be the best possible positive value and not use a negative value.
2. A single ContactPosition command changes the method used to find surface contact for both multimaterial MPM and explicit cracks (no matter which block specifies it in XML files). It is not possible to combine different position methods in a single simulation. If more than one ContactPosition command is used in the same input commands, the last one will deterimine the cutoff position
3. The ContactPosition command should always be present when all or some contacting surfaces are initially separated. Note that the command is essential for handling initially-separated surfaces that later come into contact, and it causes no problems for surfaces that start out in contact. They are still modeled correctly.
4. Although the ContactPosition method can handle all contact situations, it is usually more accurate to omit this command when all surfaces are initially in contact. Some exceptions are when the problem has large relative displacements such as sliding of a block or rolling of a disk along a surface; these actually correspond to parts of the surfaces that were separated coming into contact as the simulation evolves.
5. For irregular meshes, the absolute cutoff position will depend on the orientation of the crack. The code automatically corrects for this effect using a single input cutoff value by a method described in Nairn (2013).