FEA Periodic Boundaries
NairnFEA can solve problems with truly periodic boundary conditions in one or both directions.
Introduction
Periodic boundary conditions means to run calculations that are periodic in strain in just the x direction, just the y direction, or in both the x and y directions. For axisymmetric problems the calculations can only be periodic in the z direction. Many researchers use symmetry-based displacement conditions for periodic calculations (thinking they are periodic), but that approach cannot handle problems where plane sections do not remain plane even though the structure and strains are periodic. The periodic conditions in NairnFEA are more advanced than simple symmetry conditions and they are essential for some problems such as shear strain applied to a periodic composite material.
Theory
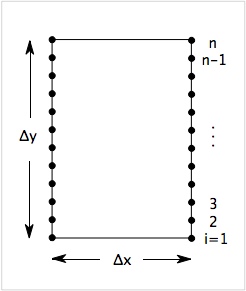
The figure on the right shows a mesh of width Δx and height Δx in which the left and right edges are parallel to the y axis and each node on the left edge corresponds to a node on the right edge at the same y coordinate. If this structure is an element on a large object and periodic in the x direction, it means the the strains are periodic or that:
[math]\displaystyle{ \varepsilon_{xx}(x+\Delta x,y) = \varepsilon_{xx}(x,y) }[/math]
[math]\displaystyle{ \varepsilon_{yy}(x+\Delta x,y) = \varepsilon_{yy}(x,y) }[/math]
[math]\displaystyle{ \gamma_{yx}(x+\Delta x,y) = \gamma_{xy}(x,y) }[/math]
These conditions are satisfied, in the most general sense, if the x and y displacements (u(x,y) and v(x,y)) have the form:
[math]\displaystyle{ u(x+\Delta x,y) = u(x,y) + k_1 + k_2 y }[/math]
[math]\displaystyle{ v(x+\Delta x,y) = v(x,y) + k_3 - k_2 x }[/math]
If there are n nodes on each edge, these conditions are satisfied if the problem is solved subjected to the following constraints:
[math]\displaystyle{ u_i(\Delta x,y_i) = u_i(0,y+i) + k_1 + k_2 y_i \qquad {\rm for}\ i=1,\ {\rm to}\ n }[/math]
[math]\displaystyle{ v_i(\Delta x,y_i) = v_i(0,y+i) + v_1(\Delta x,y_1) - v_1(0,y_1) \qquad {\rm for}\ i=2,\ {\rm to}\ n }[/math]
These conditions are solved by using FEA method of Lagrangian multipliers. All x displacements on the right are replaced by constraints as are all y (except v_1(Δx,y_1), which remains a degree of freedom. In addition, k1 and k2 are introduced as two new degrees of freedom. It is better to rewrite these degrees of freedom using
[math]\displaystyle{ k_1 + k_2 y_i = \Delta u + {du\over dy}(y_i - \left\langle y\right\rangle) }[/math]
where <y> is the mean y on the edges. Physically, Δu the mean displacement jump across the modeled object, which results in an average x direction strain:
[math]\displaystyle{ \left\langle \varepsilon_{xx}\right\rangle = {\Delta u\over \Delta x} }[/math]
Physically du/dy is the slope (or rotation) of the right edge relative to the left edge. Like nodal displacements, these new constants resulting from periodic boundary conditions can be degrees of freedom (i.e., output of the analysis) or can be inputs (e.g., boundary conditions that impose an average strain or relative rotation to the edges)
Using the same analysis on problems that are periodic only in the y (or the Z of axisymmetric analysis) give a series of constraints to displacements on the nodes at the top of the object relative to the displacements on the bottom of the object. The new constraints lead to two new degrees of freedom - Δv and dvdx. Physically, Δv is the mean displacement jump across the modeled object, which results in an average y direction strain:
[math]\displaystyle{ \left\langle \varepsilon_{yy}\right\rangle = {\Delta v\over \Delta y} }[/math]
Physically dv/dx is the slope (or rotation) of the top edge relative to the bottom edge.
Finally, if the problem is periodic in both direction, the four new degrees of freedom relate to average axial strains (as defined above for each direction) and to average shear strain by:
[math]\displaystyle{ \left\langle \gamma_{xy}\right\rangle = {1\over \Delta y}{du\over dy} + {1\over \Delta x}{dv\over dx} }[/math]
For axisymmetric problems, the model cannot be periodic in the R direction. It can be periodic in the Z direction, but to maintain periodicity in the hoop stress (εθθ) to top and bottom edges must remain aligned. In other words, the rotational degree of freedom (dw/dr) must be zero (i.e., it is not a degree of freedom). The average axial strain is related to Δw or the displacement drop in the vertical direction:
[math]\displaystyle{ \left\langle \varepsilon_{ZZ}\right\rangle = {\Delta w\over \Delta Z} }[/math]
Input Commands
In scripted files, you set up periodic boundary conditions with one or two Periodic commands:
Periodic (dir),<(dof1),(value1)>, <(dof2),(value2)>
In XML, the one or two commands, which must be in the <GridBCs section, are:
<Periodic dof='(dir)' delta='(value1)' slope='(value2)'/>
where
- (dir) defines the periodic direction. NairnFEA allows periodicity in the x direction only, in the y direction only, or in both the x and y directions. For axisymmetric problems, periodicity is allowed in the Z direction only.
- (dof1),(value1) and (dof2),(value2)
Pairs of subsequent arguments specify options to the periodic calculations. In periodic calculations, the displacements on the two edges must be related by a translation and a rotation or a translation and shear. If nothing is specified, the translation and rotation or shear are degrees of freedom in the problem. Alternatively, you can specify them with the options:
Delta: defines the translation or displacement jump between the two sides of the periodic direction (entered in mm). When applied to the x direction, the global average strain is <εxx> = Delta/Δx. When applied to the y direction, the global average strain is <εyy> = Delta/Δy. When applied to the z direction in axisymmetric analyses, the global average strain is <εzz> = Delta/Δz. Here Δx, Δy, and Δz are the specimen lengths in those directions.
Slope: When periodic in only one direction, Slope defines the rotation or relative slopes between the two sides of the periodic direction (dimensionless). When periodic in both x and y directions, Slope is a synonym for Shear (see below). For axisymmetric analyses, physical contraints require the slope to be zero. If you do not set it, it will automatically be set to zero for you.
Shear: When periodic in both x and y directions, Shear defines a component of average shear displacement. For #1 = x, Shear gives the x-direction displacement jump in the y direction of the specimen (dudy). For #2 = y, Shear gives the y-direction displacement jump in the x direction of the specimen (dvdx). The average shear strain is <γxy> = dudy/Δy + dvdx/Δx. Here Δx and Δy are the specimen lengths in those directions. When periodic in only one direction, Shear is a synonym for Slope (see above).
The dof attribute defines the periodic direction. It must be x (or 1) or y (or 2) or z (or 3). The delta, slope, and shear attributes let you specify an average displacement jump, rotation, and/or shear between the two ends in the periodic direction(s). If any are left unspecified, they will be degrees of freedom. When specified, they correspond to globally applied strains or rotation. The meanings of the parameters are slightly different depending on whether just one direction or both directions are periodic:
Notes
- Adding periodicity will greatly increase the bandwidth of the problem. A Resequence Command can be used, but is unlikely to help much. Instead, only use periodic conditions if they are needed to solve the problem.