Difference between revisions of "Coupled Traction Law"
| Line 6: | Line 6: | ||
[[File:Exptraction.jpg|right]] | [[File:Exptraction.jpg|right]] | ||
This [[Traction Laws|traction law]] uses either the [[Triangular Traction Law|triangular cohesive law]] or the [[Exponential Traction Law|exponential cohesive law]] but couples the normal and tangential displacements by | This [[Traction Laws|traction law]] uses either the [[Triangular Traction Law|triangular cohesive law]] or the [[Exponential Traction Law|exponential cohesive law]] but couples the normal and tangential displacements by using an ''effective'' displacement. This implementation follows methods derived in a paper by Högberg <ref name="hogberg"/>. | ||
The Högberg effective displacement is defined by | The Högberg effective displacement is defined by | ||
| | ||
<math> \lambda = \sqrt{\left(\frac{u_n}{\delta_c^{(n)}}\right)^2 +\left(\frac{u_t}{\delta_c^{(t)}}\right)^2}</math> | <math>\lambda = \sqrt{\left(\frac{u_n}{\delta_c^{(n)}}\right)^2 +\left(\frac{u_t}{\delta_c^{(t)}}\right)^2}</math> | ||
where u is displacement, δ<sub>c</sub> is displacement at failure (see figure), and "n" and "t" refer to normal an tangential directions. In terms of λ, the normal an tangential tractions are: | |||
| |||
<math>\left(T^{(n)},T^{(t)}\right) = \frac{H(\lambda_\omega)}{\lambda_\omega} | |||
\left(\frac{\sigma_{c}^{(n)} u_n}{\delta_c^{(n)}},\frac{\sigma_{c}^{(t)} u_t}{\delta_c^{(t)}}\right)</math> | |||
where λ<sub>\omega;</sub> is a damage parameter equal to the maximum value of λ during a simulation. | |||
These traction apply after initiation that occurs when λ reaches λ<sub>p</sub>(θ) defined by | |||
| |||
<math>\frac{1}{ \lambda_p(\theta)} = \sqrt{\left(\frac{\delta_c^{(n)}\sin\theta}{\delta_e^{(n)}}\right)^2 | |||
+ \left(\frac{\delta_c^{(t)}\cos\theta}{\delta_e^{(t)}}\right)^2} | |||
\quad {\rm with} \quad \theta = \frac{\delta_c^{(t)}u_n}{\delta_c^{(n)}u_t}</math> | |||
and δ<sub>e</sub> is displacement at end of the elastic regime. Finally, Högberg assumed H(λ) is defined by linear decay from 1 when λ=λ<sub>p</sub>(θ) to zero when λ=1: | |||
| |||
<math>H(\lambda) = \frac{1-\lambda}{1-\lambda_p(\theta)}</math> | |||
This implementation has extended the Höberg approach to also allow an exponential decay using: | |||
| |||
<math>H(\lambda) = \frac{e^{-\alpha\frac{\lambda-\lambda_p(\theta)}{1-\lambda_p(\theta)}}-e^{-\alpha}}{1-e^{-\alpha}}</math> | |||
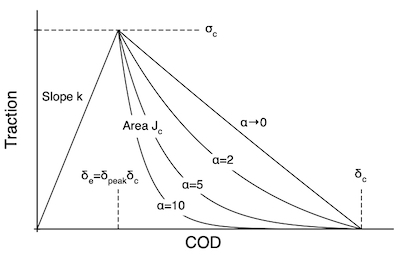
See figure above for effect of α on the decay rate (note that α=0 is identical to linear decay). | |||
Revision as of 12:16, 29 December 2020
The Traction Law
(This documentation is implementation of this law OSParticulas that is coming soon to NairnMPM. The current implementation in NairnMPM is different and should not be used until updated to this new implementation).
This traction law uses either the triangular cohesive law or the exponential cohesive law but couples the normal and tangential displacements by using an effective displacement. This implementation follows methods derived in a paper by Högberg [1].
The Högberg effective displacement is defined by
[math]\displaystyle{ \lambda = \sqrt{\left(\frac{u_n}{\delta_c^{(n)}}\right)^2 +\left(\frac{u_t}{\delta_c^{(t)}}\right)^2} }[/math]
where u is displacement, δc is displacement at failure (see figure), and "n" and "t" refer to normal an tangential directions. In terms of λ, the normal an tangential tractions are:
[math]\displaystyle{ \left(T^{(n)},T^{(t)}\right) = \frac{H(\lambda_\omega)}{\lambda_\omega} \left(\frac{\sigma_{c}^{(n)} u_n}{\delta_c^{(n)}},\frac{\sigma_{c}^{(t)} u_t}{\delta_c^{(t)}}\right) }[/math]
where λ\omega; is a damage parameter equal to the maximum value of λ during a simulation. These traction apply after initiation that occurs when λ reaches λp(θ) defined by
[math]\displaystyle{ \frac{1}{ \lambda_p(\theta)} = \sqrt{\left(\frac{\delta_c^{(n)}\sin\theta}{\delta_e^{(n)}}\right)^2 + \left(\frac{\delta_c^{(t)}\cos\theta}{\delta_e^{(t)}}\right)^2} \quad {\rm with} \quad \theta = \frac{\delta_c^{(t)}u_n}{\delta_c^{(n)}u_t} }[/math]
and δe is displacement at end of the elastic regime. Finally, Högberg assumed H(λ) is defined by linear decay from 1 when λ=λp(θ) to zero when λ=1:
[math]\displaystyle{ H(\lambda) = \frac{1-\lambda}{1-\lambda_p(\theta)} }[/math]
This implementation has extended the Höberg approach to also allow an exponential decay using:
[math]\displaystyle{ H(\lambda) = \frac{e^{-\alpha\frac{\lambda-\lambda_p(\theta)}{1-\lambda_p(\theta)}}-e^{-\alpha}}{1-e^{-\alpha}} }[/math]
See figure above for effect of α on the decay rate (note that α=0 is identical to linear decay).
except that COD and traction are now effective terms that are related to normal and tangential components of traction and displacement:
[math]\displaystyle{ {\rm Traction} = T_{eff} \qquad{\rm where} \qquad T_{eff} = \sqrt{T_n^2+T_t^2} }[/math]
[math]\displaystyle{ {\rm cod} = \delta_{eff} \qquad{\rm where} \qquad \delta_{eff} = \sqrt{\delta_n^2+\delta_t^2} }[/math]
where Tn and Tt are the normal and tangential tractions and δn and δt are the normal and tangential CODs.
This law can be expressed using damage mechanics by defining an effective slope of
[math]\displaystyle{ k_{eff}=(1-D)k }[/math]
where k is the initial slope of the curve and D is a damage parameter. This effective slope describes a line from the origin to the point on the triangular curve corresponding to the maximum displacement seen on the current particle. The effective traction along that line is
[math]\displaystyle{ T_{eff}=k_{eff}\delta_{eff} }[/math]
The effective stiffness is found using
[math]\displaystyle{ (1-D)={\delta_{pk}(\delta_c-\delta_{max})\over\delta_{max}(\delta_c-\delta_{pk})} }[/math]
where δc is the critical effective cod and δmax is the maximum effective cod seen on the crack particle, except that it is initialized to the peak cod (δpk) at the start of the calculations. By this relation, D = 0 until the effective cod passes the peak cod. Thereafter, D increases from 0 at the peak to 1 at the critical cod. Once D is found, the normal and tangential tractions are:
[math]\displaystyle{ T_n = k_{eff}\delta_n \qquad {\rm and} \qquad T_t = k_{eff}\delta_t }[/math]
Together, these traction satisfy the effective traction - effective cod law given above. Note that during monotonic loading the traction will remain on the curve. If unloading occurs, however, the tractions follow a line back to the original from the maximum cod.
Failure
Under pure mode I or pure mode II, a coupled traction law and its failure are identical to a triangular traction law. Under mixed-mode conditions, however, the two laws differ and therefore provide two alternatives to modeling of mixed mode behavior. The use of effective terms in this coupled law is proposed to account for mixed mode effects with a single traction law. A potential concern, however, is that this law introduces history dependence in fracture experiments that may contradict observations in real materials.
Alternate Effective Displacement Method
Traction Law Properties
The properties you enter are the same as defined in
References
- ↑ J. L. H ögberg, "Mixed mode cohesive law," International Journal of Fracture, 141, 549–559 (2006).
- ↑ P. P. Camanho and C. G. Dàvila, "Mixed-mode decohesion finite elements for the simulation of delamination in composite materials," Technical Report, NASA/TM-2002-211737 (2002).
- ↑ G. T. Camacho and M. Ortiz, "Computational modelling of impact damage in brittle materials," Int. J. Solids Struct., 33, 2899–2938 (1996).
Cite error: <ref> tag with name "mmzone" defined in <references> is not used in prior text.