Difference between revisions of "Coupled Traction Law"
| (46 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== The Traction Law == | == The Traction Law == | ||
[[File: | [[File:Exptraction.jpg|right]] | ||
This [[Traction Laws|traction law]] | This [[Traction Laws|traction law]] uses either the [[Triangular Traction Law|triangular cohesive law]] or the [[Exponential Traction Law|exponential cohesive law]] but couples the normal and tangential displacements by using an ''effective'' displacement. This implementation follows methods derived in a paper by Högberg.<ref name="hogberg"/> The Högberg effective displacement is defined by | ||
| | ||
<math> {\ | <math>\lambda = \sqrt{\left(\frac{u_n}{\delta_c^{(n)}}\right)^2 +\left(\frac{u_t}{\delta_c^{(t)}}\right)^2}</math> | ||
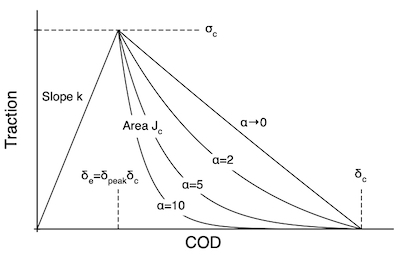
where u is displacement, δ<sub>c</sub> is displacement at failure (see figure), and "n" and "t" refer to normal an tangential directions. In terms of λ, the normal and tangential tractions are: | |||
| |||
<math>\left(T^{(n)},T^{(t)}\right) = \frac{H(\lambda_\omega)}{\lambda_\omega} | |||
\left(\frac{\sigma_{c}^{(n)} u_n}{\delta_c^{(n)}},\frac{\sigma_{c}^{(t)} u_t}{\delta_c^{(t)}}\right)</math> | |||
where λ<sub>ω</sub> is a damage parameter equal to the maximum value of λ during a simulation. | |||
These traction apply after initiation and correctly account for elastic unloading and reloading. Prior to initiation, deformations are elastic. Initiation using an elliptical failure criterion occurs when λ reaches λ<sub>p</sub>(θ) defined by | |||
| |||
<math>\frac{1}{ \lambda_p(\theta)} = \sqrt{\left(\frac{\delta_c^{(n)}\sin\theta}{\delta_e^{(n)}}\right)^2 | |||
+ \left(\frac{\delta_c^{(t)}\cos\theta}{\delta_e^{(t)}}\right)^2} | |||
\quad {\rm with} \quad \theta = \frac{\delta_c^{(t)}u_n}{\delta_c^{(n)}u_t}</math> | |||
and δ<sub>e</sub> is displacement at end of the elastic regime.<ref name="hogberg"/> Finally, Högberg assumed H(λ) is defined by linear decay from 1 when λ=λ<sub>p</sub>(θ) to zero when λ=1: | |||
| | ||
<math> | <math>H(\lambda) = \frac{1-\lambda}{1-\lambda_p(\theta)}</math> | ||
This implementation has extended the Höberg approach to also allow an exponential decay using: | |||
| |||
<math>H(\lambda) = \frac{e^{-\alpha\frac{\lambda-\lambda_p(\theta)}{1-\lambda_p(\theta)}}-e^{-\alpha}}{1-e^{-\alpha}}</math> | |||
See figure above for effect of α on the decay rate (note that α approaching zero is identical to linear decay). | |||
== Failure == | == Failure == | ||
Under pure mode I or pure mode II, a coupled traction law and its failure are identical to a [[Triangular Traction Law|triangular cohesive law]] or an [[Exponential Traction Law|exponential cohesive law]]. Under mixed-mode conditions, however, these laws differ. [[Triangular Traction Law|Triangular]] and [[Exponential Traction Law|exponential]] cohesive law have to impose a [[Triangular Traction Law#Failure|mixed-mode failure criterion]]. This model does not need such a criterion. It fails naturally when λ reaches one. Despite this advantage of failing "naturally", the Högberg model<ref name="hogberg"/> has limitations explained in the next section. | |||
== Property Limitations == | |||
The Höberg model<ref name="hogberg"/> seemingly depends on independent normal and traction law properties that could be entered as for [[Triangular Traction Law|triangular]] or the [[Exponential Traction Law|exponential]] cohesive laws. In fact Ref. <ref name="hogberg"/> claims independent properties are allowed. A new analysis of cohesive zone modeling,<ref name="mixedmode"/> however, has revealed that the Högberg model is always invalid for mixed-mode loading unless properties are chosen such that | |||
| |||
<math>\frac{\delta_e^{(n)}}{\delta_c^{(n)}} = \frac{\delta_e^{(t)}}{\delta_c^{(t)}}</math> | |||
In other words, the ratio of displacement at peak stress to displacment and failure must be the same for both normal and tangential directions. When using the exponential extension of the Högberg model the α coefficient must also be the same for normal and tangential directions. | |||
Note that this implementation lets you [[#Traction Law Properties|choose properties]] that make the modeling invalid. That option is allowed for comparison of the published model to other models. If you do select invalid properties, the output file will include a warning. The preferred model for simulations of mixed-mode failure, which remains valid for independent normal and tangential laws, is the [[Mixed Mode Traction Law]]. | |||
== Alternate Effective Displacement Method == | |||
Other mixed-mode cohesive laws have used unscaled ''effective'' displacement models or simply define it is magnitude of the crack opening displacement: | |||
| |||
<math>\lambda = \sqrt{u_n^2+u_t^2}</math> | |||
Examples are found in Comanho and Dàvila<ref name="comanho"/> and Comacho and Ortiz<ref name="comacho"/> (these models are implemented in Abaqus cohesive elements). These models are not separately implementeded in [[NairnMPM]] because they are superfluous. They can be used with this model simply by choosing | |||
| |||
<math>\delta_c^{(n)} = \delta_c^{(t)}</math> | |||
Combining this restriction with the [[#Property Limitations|Högerg limitation]], means this alternate effective displacement model is invalid unless: | |||
| |||
<math>\frac{\delta_e^{(n)}}{\delta_e^{(t)}} = \frac{\delta_c^{(n)}}{\delta_c^{(t)}} = 1</math> | |||
or both elastic and critical displacements in the normal and tangential cohesive laws are identical (the law magnitudes, or normal and tangential strengths, can differ). Implementations of this approach, such as in Abaqus, unfortunately let users select properties that invalidate the modeling. | |||
== Traction Law Properties == | == Traction Law Properties == | ||
The following properties are used to create a | The following properties are used to create a coupled traction law: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 24: | Line 77: | ||
! Property !! Description !! Units !! Default | ! Property !! Description !! Units !! Default | ||
|- | |- | ||
| ([[ | | ([[Triangular Traction Law#Traction Law Properties|Triangular Laws]]) || Enter properties to define normal and tangential cohesive laws assuming triangular traction laws || varies || none | ||
|- | |||
| model || Choose whether to model using linear decay (12) or exponential decay (34). The numerical values are material IDs for linear and exponential [[Traction Laws#Traction Law Materials|traction laws]] || none || 12 | |||
|- | |||
| alpha || When using exponential decay (model=34), this parameter selects the α coefficient for the decay rate. Note that when using exponential decay, this implementation first finds law properties assuming triangular traction laws and then recalculates G<sub>c</sub> based on triangular values or stress and displacements. || none || none | |||
|} | |} | ||
As [[#Property Limitations|described above]], this implementation lets you select properties that invalidate the method when used to model mixed-mode failure. If you choose invalid properties, a warning is printed in the output files. | |||
== Traction History Variables == | |||
This material tracks the following traction history variables | |||
# Maximum value of λ (or λ<sub>ω</sub> (the value is <0 until initiation of damage) | |||
# Cumulative work energy | |||
# Normal crack opening displacement (u<sub>n</sub>) | |||
# Tangential crack opening displacement (u<sub>t</sub>) | |||
These history variables can be [[MPM Archiving Options#ToArchive Command|archived]] for later plotting. The [[MPM Archiving Options#ToArchive Command|cmdisp archiving option]] can archive total mode I and mode II cumulative dissipated energies. | |||
== References == | |||
<references> | |||
<ref name="hogberg">J. L. H ögberg, "Mixed mode cohesive law," <i>International Journal of Fracture</i>, <b>141</b>, 549–559 (2006).</ref> | |||
<ref name="mixedmode">J. A. Nairn and Y. E. Aimene "A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws" <i>in preparation</i> (2020).</ref> | |||
<ref name="comanho">P. P. Camanho and C. G. Dàvila, "Mixed-mode decohesion finite elements for the simulation of delamination in composite materials," Technical Report, NASA/TM-2002-211737 (2002).</ref> | |||
<ref name="comacho">G. T. Camacho and M. Ortiz, "Computational modelling of impact damage in brittle materials," <i>Int. J. Solids Struct.</i>, <b>33</b>, 2899–2938 (1996).</ref> | |||
</references> | |||
Latest revision as of 23:03, 2 January 2021
The Traction Law
This traction law uses either the triangular cohesive law or the exponential cohesive law but couples the normal and tangential displacements by using an effective displacement. This implementation follows methods derived in a paper by Högberg.[1] The Högberg effective displacement is defined by
[math]\displaystyle{ \lambda = \sqrt{\left(\frac{u_n}{\delta_c^{(n)}}\right)^2 +\left(\frac{u_t}{\delta_c^{(t)}}\right)^2} }[/math]
where u is displacement, δc is displacement at failure (see figure), and "n" and "t" refer to normal an tangential directions. In terms of λ, the normal and tangential tractions are:
[math]\displaystyle{ \left(T^{(n)},T^{(t)}\right) = \frac{H(\lambda_\omega)}{\lambda_\omega} \left(\frac{\sigma_{c}^{(n)} u_n}{\delta_c^{(n)}},\frac{\sigma_{c}^{(t)} u_t}{\delta_c^{(t)}}\right) }[/math]
where λω is a damage parameter equal to the maximum value of λ during a simulation. These traction apply after initiation and correctly account for elastic unloading and reloading. Prior to initiation, deformations are elastic. Initiation using an elliptical failure criterion occurs when λ reaches λp(θ) defined by
[math]\displaystyle{ \frac{1}{ \lambda_p(\theta)} = \sqrt{\left(\frac{\delta_c^{(n)}\sin\theta}{\delta_e^{(n)}}\right)^2 + \left(\frac{\delta_c^{(t)}\cos\theta}{\delta_e^{(t)}}\right)^2} \quad {\rm with} \quad \theta = \frac{\delta_c^{(t)}u_n}{\delta_c^{(n)}u_t} }[/math]
and δe is displacement at end of the elastic regime.[1] Finally, Högberg assumed H(λ) is defined by linear decay from 1 when λ=λp(θ) to zero when λ=1:
[math]\displaystyle{ H(\lambda) = \frac{1-\lambda}{1-\lambda_p(\theta)} }[/math]
This implementation has extended the Höberg approach to also allow an exponential decay using:
[math]\displaystyle{ H(\lambda) = \frac{e^{-\alpha\frac{\lambda-\lambda_p(\theta)}{1-\lambda_p(\theta)}}-e^{-\alpha}}{1-e^{-\alpha}} }[/math]
See figure above for effect of α on the decay rate (note that α approaching zero is identical to linear decay).
Failure
Under pure mode I or pure mode II, a coupled traction law and its failure are identical to a triangular cohesive law or an exponential cohesive law. Under mixed-mode conditions, however, these laws differ. Triangular and exponential cohesive law have to impose a mixed-mode failure criterion. This model does not need such a criterion. It fails naturally when λ reaches one. Despite this advantage of failing "naturally", the Högberg model[1] has limitations explained in the next section.
Property Limitations
The Höberg model[1] seemingly depends on independent normal and traction law properties that could be entered as for triangular or the exponential cohesive laws. In fact Ref. [1] claims independent properties are allowed. A new analysis of cohesive zone modeling,[2] however, has revealed that the Högberg model is always invalid for mixed-mode loading unless properties are chosen such that
[math]\displaystyle{ \frac{\delta_e^{(n)}}{\delta_c^{(n)}} = \frac{\delta_e^{(t)}}{\delta_c^{(t)}} }[/math]
In other words, the ratio of displacement at peak stress to displacment and failure must be the same for both normal and tangential directions. When using the exponential extension of the Högberg model the α coefficient must also be the same for normal and tangential directions.
Note that this implementation lets you choose properties that make the modeling invalid. That option is allowed for comparison of the published model to other models. If you do select invalid properties, the output file will include a warning. The preferred model for simulations of mixed-mode failure, which remains valid for independent normal and tangential laws, is the Mixed Mode Traction Law.
Alternate Effective Displacement Method
Other mixed-mode cohesive laws have used unscaled effective displacement models or simply define it is magnitude of the crack opening displacement:
[math]\displaystyle{ \lambda = \sqrt{u_n^2+u_t^2} }[/math]
Examples are found in Comanho and Dàvila[3] and Comacho and Ortiz[4] (these models are implemented in Abaqus cohesive elements). These models are not separately implementeded in NairnMPM because they are superfluous. They can be used with this model simply by choosing
[math]\displaystyle{ \delta_c^{(n)} = \delta_c^{(t)} }[/math]
Combining this restriction with the Högerg limitation, means this alternate effective displacement model is invalid unless:
[math]\displaystyle{ \frac{\delta_e^{(n)}}{\delta_e^{(t)}} = \frac{\delta_c^{(n)}}{\delta_c^{(t)}} = 1 }[/math]
or both elastic and critical displacements in the normal and tangential cohesive laws are identical (the law magnitudes, or normal and tangential strengths, can differ). Implementations of this approach, such as in Abaqus, unfortunately let users select properties that invalidate the modeling.
Traction Law Properties
The following properties are used to create a coupled traction law:
| Property | Description | Units | Default |
|---|---|---|---|
| (Triangular Laws) | Enter properties to define normal and tangential cohesive laws assuming triangular traction laws | varies | none |
| model | Choose whether to model using linear decay (12) or exponential decay (34). The numerical values are material IDs for linear and exponential traction laws | none | 12 |
| alpha | When using exponential decay (model=34), this parameter selects the α coefficient for the decay rate. Note that when using exponential decay, this implementation first finds law properties assuming triangular traction laws and then recalculates Gc based on triangular values or stress and displacements. | none | none |
As described above, this implementation lets you select properties that invalidate the method when used to model mixed-mode failure. If you choose invalid properties, a warning is printed in the output files.
Traction History Variables
This material tracks the following traction history variables
- Maximum value of λ (or λω (the value is <0 until initiation of damage)
- Cumulative work energy
- Normal crack opening displacement (un)
- Tangential crack opening displacement (ut)
These history variables can be archived for later plotting. The cmdisp archiving option can archive total mode I and mode II cumulative dissipated energies.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 J. L. H ögberg, "Mixed mode cohesive law," International Journal of Fracture, 141, 549–559 (2006).
- ↑ J. A. Nairn and Y. E. Aimene "A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws" in preparation (2020).
- ↑ P. P. Camanho and C. G. Dàvila, "Mixed-mode decohesion finite elements for the simulation of delamination in composite materials," Technical Report, NASA/TM-2002-211737 (2002).
- ↑ G. T. Camacho and M. Ortiz, "Computational modelling of impact damage in brittle materials," Int. J. Solids Struct., 33, 2899–2938 (1996).