Difference between revisions of "FEA Periodic Boundaries"
(→Theory) |
|||
| (34 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[NairnFEA]] can solve problems with truly periodic boundary conditions in one or both directions. | |||
== Introduction == | == Introduction == | ||
| Line 7: | Line 8: | ||
[[File:Periodic.jpg|right]] | [[File:Periodic.jpg|right]] | ||
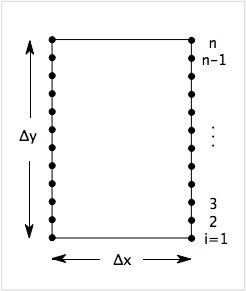
The figure shows a mesh of width Δx and height Δ | The figure on the right shows a mesh of width Δx and height Δy in which the left and right edges are parallel to the <tt>y</tt> axis and each node on the left edge corresponds to a node on the right edge at the same <tt>y</tt> coordinate. If this structure is a piece on a large object that is periodic in the <tt>x</tt> direction only, it means that the strains are periodic or that: | ||
| | ||
<math> \varepsilon_{xx}(x+\Delta x,y) = \varepsilon_{xx}(x,y) | <math> \varepsilon_{xx}(x+\Delta x,y) = \varepsilon_{xx}(x,y)</math> | ||
| |||
<math>\varepsilon_{yy}(x+\Delta x,y) = \varepsilon_{yy}(x,y)</math> | |||
| |||
<math>\gamma_{yx}(x+\Delta x,y) = \gamma_{xy}(x,y)</math> | |||
These conditions are satisfied, in the most general sense, if the <tt>x</tt> and <tt>y</tt> displacements (<tt>u(x,y)</tt> and <tt>v(x,y)</tt>) have the form: | These conditions are satisfied, in the most general sense, if the <tt>x</tt> and <tt>y</tt> displacements (<tt>u(x,y)</tt> and <tt>v(x,y)</tt>) have the form: | ||
| | ||
<math>u(x+\Delta x,y) = u(x,y) + k_1 + k_2 y | <math>u(x+\Delta x,y) = u(x,y) + k_1 + k_2 y</math> | ||
| |||
<math>v(x+\Delta x,y) = v(x,y) + k_3 - k_2 x</math> | |||
If there are n nodes on each edge, these conditions are satisfied if the problem is solved subjected to the following constraints: | If there are n nodes on each edge, these conditions are satisfied if the problem is solved subjected to the following constraints: | ||
| | ||
<math>u_i(\Delta x,y_i) = u_i(0, | <math>u_i(\Delta x,y_i) = u_i(0,y_i) + k_1 + k_2 y_i \qquad {\rm for}\ i=1,\ {\rm to}\ n</math> | ||
| |||
<math>v_i(\Delta x,y_i) = v_i(0,y_i) + v_1(\Delta x,y_1) - v_1(0,y_1) \qquad {\rm for}\ i=2,\ {\rm to}\ n</math> | |||
These conditions are solved by using FEA method of Lagrange multipliers. All <tt>x</tt> displacements on the right are replaced by constraints as are all <tt>y</tt> (except <math>v_1(\Delta x,y_1)</math>, which remains a degree of freedom). In addition, k<sub>1</sub> and k<sub>2</sub> are introduced as two new degrees of freedom. It is better to rewrite new degrees of freedom using | |||
| | ||
<math> | <math>k_1 + k_2 y_i = \Delta u_n + {\Delta u_s\over \Delta y}(y_i - \left\langle y\right\rangle)</math> | ||
where <<tt>y</tt>> is the mean <tt>y</tt> on the edges. Physically, Δu<sub>n</sub> is the mean displacement jump in the x direction across the modeled object, which results in an average <tt>x</tt> direction strain: | |||
| | ||
<math> | <math>\left\langle \varepsilon_{xx}\right\rangle = {\Delta u_n\over \Delta x}</math> | ||
Similarly, Δu<sub>s</sub> the shear jump in the x direction or the difference in x direction jumps at the top and bottom of the object. Like nodal displacements, these new terms resulting from periodic boundary conditions can be degrees of freedom (''i.e.'', output of the analysis) or can be inputs (''e.g.'', boundary conditions that impose an average stretch or shear displacement to the edges). | |||
Using the same analysis on problems that are periodic only in the <tt>y</tt> (or the <tt>Z</tt> of axisymmetric analysis) direction gives a series of constraints for displacements on the nodes at the top of the object relative to the displacements on the bottom edge. The new constraints lead to two more degrees of freedom - Δv<sub>n</sub> and Δv<sub>s</sub>. Physically, Δv<sub>n</sub> is the mean displacement jump across the modeled object, which results in an average <tt>y</tt> direction strain: | |||
| | ||
<math>\left\langle \varepsilon_{ | <math>\left\langle \varepsilon_{yy}\right\rangle = {\Delta v_n\over \Delta y}</math> | ||
Similarly, Δv<sub>s</sub> the shear jump in the y direction or the difference in y direction jumps at the left and right of the object. | |||
If both directions are periodic, the analysis needs some modifications. The general displacement constraints between left and right or top and bottom edges can be written: | |||
| |||
<math>u_i(\Delta x,y_i) = u_i(0,y_i) + \left\langle \varepsilon_{xx}\right\rangle \Delta x = u_i(0,y_i) + \Delta u_n</math> | |||
| |||
<math>v_i(\Delta x,y_i) = v_i(0,y_i) + \left({\left\langle\gamma_{xy}\right\rangle\over 2} - \omega\right) \Delta x = v_i(0,y_i) + \Delta v_s</math> | |||
| | ||
<math>\left\langle \ | <math>u_i(x_i,\Delta y) = u_i(x_i,0) + \left({\left\langle \gamma_{xy}\right\rangle\over 2} + \omega\right) \Delta y = u_i(x_i,0) + \Delta u_s</math> | ||
| |||
<math>v_i(x_i,\Delta y) = v_i(x_i,0) + \left\langle \varepsilon_{yy}\right\rangle \Delta y = v_i(x_i,0) + \Delta v_n</math> | |||
where ω is a rigid body rotation. The average normal strains are as above. The average shear strain is | |||
| | ||
<math>\left\langle \gamma_{xy}\right\rangle = { | <math>\left\langle \gamma_{xy}\right\rangle = {\Delta u_s\over \Delta y} + {\Delta v_s\over \Delta x}</math> | ||
For axisymmetric problems, the model cannot be periodic in the <tt>R</tt> direction. It can be periodic in the <tt>Z</tt> direction, but to maintain periodicity in the hoop stress (ε<sub>θθ</sub>) | For axisymmetric problems, the model cannot be periodic in the <tt>R</tt> direction. It can be periodic in the <tt>Z</tt> direction, but to maintain periodicity in the hoop stress (ε<sub>θθ</sub>), the top and bottom edges must not rotate. In other words, the shear stretch (Δv<sub>s</sub>) must be zero (''i.e.'', it is not a degree of freedom). The average axial strain is related to Δw<sub>n</sub> or the displacement jump in the vertical direction: | ||
| | ||
<math>\left\langle \varepsilon_{ZZ}\right\rangle = {\Delta | <math>\left\langle \varepsilon_{ZZ}\right\rangle = {\Delta w_n\over \Delta Z}</math> | ||
== Input Commands == | == Input Commands == | ||
The < | In scripted files, you set up periodic boundary conditions with one or two <tt>Periodic</tt> commands: | ||
Periodic (dir),<(dof1),(value1)>,<(dof2),(value2)> | |||
In <tt>XML</tt>, the one or two commands, which must be in the [[FEA Boundary Conditions#XML Input Files|<tt><GridBCs></tt> block]], are: | |||
<Periodic dof='(dir)' delta='(value1)' slope='(value2)'/> | |||
where | |||
* <tt>(dir)</tt> defines the periodic direction. [[NairnFEA]] allows periodicity in the <tt>x</tt> direction only, in the <tt>y</tt> direction only, or in both the <tt>x</tt> and <tt>y</tt> directions. For axisymmetric problems, periodicity is allowed in the <tt>Z</tt> direction only. | |||
* The optional <tt>(dof1),(value1)</tt> and <tt>(dof2),(value2)</tt> in scripted files can fix one or two periodic boundary degrees of freedom. In each pair, the <tt>dof</tt> is the degree or freedom and <tt>value</tt> is the setting. The options for <tt>dof</tt> are: | |||
*# <tt>Delta</tt> to set the displacement jump in that direction (in [[ConsistentUnits Command#Legacy and Consistent Units|length units]]). When applied to the <tt>x</tt> direction, the global average strain is <ε<sub>xx</sub>> = <tt>Delta</tt>/Δx. When applied to the <tt>y</tt> direction, the global average strain is <ε<sub>yy</sub>> = <tt>Delta</tt>/Δy. When applied to the <tt>Z</tt> direction in axisymmetric analyses, the global average strain is <ε<sub>zz</sub>> = <tt>Delta</tt>/Δz. Here Δx, Δy, and Δz are the specimen lengths in those directions. | |||
*# <tt>Slope</tt> defines the relative edge slopes between the two sides when there is one periodic direction (dimensioness). It is Δu<sub>s</sub>/Δy for <tt>x</tt> direction only and Δv<sub>s</sub>/Δx for <tt>y</tt> (or <tt>Z</tt>) direction only. | |||
*# <tt>Shear</tt> defines the shearing displacement jump difference between the two sides of the periodic direction (in [[ConsistentUnits Command#Legacy and Consistent Units|length units]]) when both directions are periodic. It is Δu<sub>s</sub> for <tt>x</tt> direction setting and Δv<sub>s</sub> for <tt>y</tt> (or <tt>Z</tt>) direction setting. When periodic in both <tt>x</tt> and <tt>y</tt> directions, the average shear strain is <γ<sub>xy</sub>> = <tt>ShearX</tt>/Δy + <tt>ShearY</tt>/Δx. Here Δx and Δy are the specimen lengths in the two directions, <tt>ShearX</tt> is Δu<sub>s</sub>, and <tt>ShearY</tt> is Δv<sub>s</sub>. | |||
* In <tt>XML</tt> files, optional <tt>(value1)</tt> and <tt>(value2)</tt> set the displacement jump and rotation using <tt>delta</tt> and <tt>slope</tt>, <tt>shear</tt> attributes. | |||
For periodicity to work, the edges of the specimen on the two ends of the periodic direction(s) must be orthognal to that direction, they must each have the same number of nodes, and the orthogonal coordinate (''e.g.'', the <tt>y</tt> coordinate for <tt>x</tt> periodicity, the <tt>x</tt> coordinate for <tt>y</tt> periodicity, or the <tt>R</tt> coordinate for <tt>Z</tt> periodicity) of each node on one side must match the corresponding node on the other side. | |||
Setting the periodic degrees of freedom for <tt>Delta</tt>, <tt>Slope</tt>, and <tt>Shear</tt> are optional. If they are not set, they are degrees of freedom in the problem (and can be found from output results). If they are set as boundary conditions, they can determine the average normal strains, edge rotations, and average shear strains. Finally, scripted commands can use <tt>Slope</tt> as a synonym from <tt>Shear</tt> and <tt>XML</tt> command can use a <tt>slope</tt> attribute as a synonym for the <tt>shear</tt> attribute. The code defines the appropriately condition depending on whether one or two directions are made periodic. | |||
== Notes == | |||
# Adding periodicity will greatly increase the bandwidth of the problem. A [[Resequence Command]] can be used, but is unlikely to help much. The problem is that periodic conditions causes edge nodes to be related to displacement of nodes on the opposite end for the object. This loss of locality disrupts the resequencing algorithm, which is based on an assumption that nodes depend only on nodes in common elements. | |||
# Because periodicity increases the band width, it should only be used when needed. If the edges of a periodic problem remain planar and parallel, then the periodicity can be achieved with simple displacement boundary conditions. One way to check if this situation holds is to run with true periodic boundary conditions and check the displacements on the edges. | |||
Latest revision as of 14:19, 2 June 2015
NairnFEA can solve problems with truly periodic boundary conditions in one or both directions.
Introduction
Periodic boundary conditions means to run calculations that are periodic in strain in just the x direction, just the y direction, or in both the x and y directions. For axisymmetric problems the calculations can only be periodic in the z direction. Many researchers use symmetry-based displacement conditions for periodic calculations (thinking they are periodic), but that approach cannot handle problems where plane sections do not remain plane even though the structure and strains are periodic. The periodic conditions in NairnFEA are more advanced than simple symmetry conditions and they are essential for some problems such as shear strain applied to a periodic composite material.
Theory
The figure on the right shows a mesh of width Δx and height Δy in which the left and right edges are parallel to the y axis and each node on the left edge corresponds to a node on the right edge at the same y coordinate. If this structure is a piece on a large object that is periodic in the x direction only, it means that the strains are periodic or that:
[math]\displaystyle{ \varepsilon_{xx}(x+\Delta x,y) = \varepsilon_{xx}(x,y) }[/math]
[math]\displaystyle{ \varepsilon_{yy}(x+\Delta x,y) = \varepsilon_{yy}(x,y) }[/math]
[math]\displaystyle{ \gamma_{yx}(x+\Delta x,y) = \gamma_{xy}(x,y) }[/math]
These conditions are satisfied, in the most general sense, if the x and y displacements (u(x,y) and v(x,y)) have the form:
[math]\displaystyle{ u(x+\Delta x,y) = u(x,y) + k_1 + k_2 y }[/math]
[math]\displaystyle{ v(x+\Delta x,y) = v(x,y) + k_3 - k_2 x }[/math]
If there are n nodes on each edge, these conditions are satisfied if the problem is solved subjected to the following constraints:
[math]\displaystyle{ u_i(\Delta x,y_i) = u_i(0,y_i) + k_1 + k_2 y_i \qquad {\rm for}\ i=1,\ {\rm to}\ n }[/math]
[math]\displaystyle{ v_i(\Delta x,y_i) = v_i(0,y_i) + v_1(\Delta x,y_1) - v_1(0,y_1) \qquad {\rm for}\ i=2,\ {\rm to}\ n }[/math]
These conditions are solved by using FEA method of Lagrange multipliers. All x displacements on the right are replaced by constraints as are all y (except [math]\displaystyle{ v_1(\Delta x,y_1) }[/math], which remains a degree of freedom). In addition, k1 and k2 are introduced as two new degrees of freedom. It is better to rewrite new degrees of freedom using
[math]\displaystyle{ k_1 + k_2 y_i = \Delta u_n + {\Delta u_s\over \Delta y}(y_i - \left\langle y\right\rangle) }[/math]
where <y> is the mean y on the edges. Physically, Δun is the mean displacement jump in the x direction across the modeled object, which results in an average x direction strain:
[math]\displaystyle{ \left\langle \varepsilon_{xx}\right\rangle = {\Delta u_n\over \Delta x} }[/math]
Similarly, Δus the shear jump in the x direction or the difference in x direction jumps at the top and bottom of the object. Like nodal displacements, these new terms resulting from periodic boundary conditions can be degrees of freedom (i.e., output of the analysis) or can be inputs (e.g., boundary conditions that impose an average stretch or shear displacement to the edges).
Using the same analysis on problems that are periodic only in the y (or the Z of axisymmetric analysis) direction gives a series of constraints for displacements on the nodes at the top of the object relative to the displacements on the bottom edge. The new constraints lead to two more degrees of freedom - Δvn and Δvs. Physically, Δvn is the mean displacement jump across the modeled object, which results in an average y direction strain:
[math]\displaystyle{ \left\langle \varepsilon_{yy}\right\rangle = {\Delta v_n\over \Delta y} }[/math]
Similarly, Δvs the shear jump in the y direction or the difference in y direction jumps at the left and right of the object.
If both directions are periodic, the analysis needs some modifications. The general displacement constraints between left and right or top and bottom edges can be written:
[math]\displaystyle{ u_i(\Delta x,y_i) = u_i(0,y_i) + \left\langle \varepsilon_{xx}\right\rangle \Delta x = u_i(0,y_i) + \Delta u_n }[/math]
[math]\displaystyle{ v_i(\Delta x,y_i) = v_i(0,y_i) + \left({\left\langle\gamma_{xy}\right\rangle\over 2} - \omega\right) \Delta x = v_i(0,y_i) + \Delta v_s }[/math]
[math]\displaystyle{ u_i(x_i,\Delta y) = u_i(x_i,0) + \left({\left\langle \gamma_{xy}\right\rangle\over 2} + \omega\right) \Delta y = u_i(x_i,0) + \Delta u_s }[/math]
[math]\displaystyle{ v_i(x_i,\Delta y) = v_i(x_i,0) + \left\langle \varepsilon_{yy}\right\rangle \Delta y = v_i(x_i,0) + \Delta v_n }[/math]
where ω is a rigid body rotation. The average normal strains are as above. The average shear strain is
[math]\displaystyle{ \left\langle \gamma_{xy}\right\rangle = {\Delta u_s\over \Delta y} + {\Delta v_s\over \Delta x} }[/math]
For axisymmetric problems, the model cannot be periodic in the R direction. It can be periodic in the Z direction, but to maintain periodicity in the hoop stress (εθθ), the top and bottom edges must not rotate. In other words, the shear stretch (Δvs) must be zero (i.e., it is not a degree of freedom). The average axial strain is related to Δwn or the displacement jump in the vertical direction:
[math]\displaystyle{ \left\langle \varepsilon_{ZZ}\right\rangle = {\Delta w_n\over \Delta Z} }[/math]
Input Commands
In scripted files, you set up periodic boundary conditions with one or two Periodic commands:
Periodic (dir),<(dof1),(value1)>,<(dof2),(value2)>
In XML, the one or two commands, which must be in the <GridBCs> block, are:
<Periodic dof='(dir)' delta='(value1)' slope='(value2)'/>
where
- (dir) defines the periodic direction. NairnFEA allows periodicity in the x direction only, in the y direction only, or in both the x and y directions. For axisymmetric problems, periodicity is allowed in the Z direction only.
- The optional (dof1),(value1) and (dof2),(value2) in scripted files can fix one or two periodic boundary degrees of freedom. In each pair, the dof is the degree or freedom and value is the setting. The options for dof are:
- Delta to set the displacement jump in that direction (in length units). When applied to the x direction, the global average strain is <εxx> = Delta/Δx. When applied to the y direction, the global average strain is <εyy> = Delta/Δy. When applied to the Z direction in axisymmetric analyses, the global average strain is <εzz> = Delta/Δz. Here Δx, Δy, and Δz are the specimen lengths in those directions.
- Slope defines the relative edge slopes between the two sides when there is one periodic direction (dimensioness). It is Δus/Δy for x direction only and Δvs/Δx for y (or Z) direction only.
- Shear defines the shearing displacement jump difference between the two sides of the periodic direction (in length units) when both directions are periodic. It is Δus for x direction setting and Δvs for y (or Z) direction setting. When periodic in both x and y directions, the average shear strain is <γxy> = ShearX/Δy + ShearY/Δx. Here Δx and Δy are the specimen lengths in the two directions, ShearX is Δus, and ShearY is Δvs.
- In XML files, optional (value1) and (value2) set the displacement jump and rotation using delta and slope, shear attributes.
For periodicity to work, the edges of the specimen on the two ends of the periodic direction(s) must be orthognal to that direction, they must each have the same number of nodes, and the orthogonal coordinate (e.g., the y coordinate for x periodicity, the x coordinate for y periodicity, or the R coordinate for Z periodicity) of each node on one side must match the corresponding node on the other side.
Setting the periodic degrees of freedom for Delta, Slope, and Shear are optional. If they are not set, they are degrees of freedom in the problem (and can be found from output results). If they are set as boundary conditions, they can determine the average normal strains, edge rotations, and average shear strains. Finally, scripted commands can use Slope as a synonym from Shear and XML command can use a slope attribute as a synonym for the shear attribute. The code defines the appropriately condition depending on whether one or two directions are made periodic.
Notes
- Adding periodicity will greatly increase the bandwidth of the problem. A Resequence Command can be used, but is unlikely to help much. The problem is that periodic conditions causes edge nodes to be related to displacement of nodes on the opposite end for the object. This loss of locality disrupts the resequencing algorithm, which is based on an assumption that nodes depend only on nodes in common elements.
- Because periodicity increases the band width, it should only be used when needed. If the edges of a periodic problem remain planar and parallel, then the periodicity can be achieved with simple displacement boundary conditions. One way to check if this situation holds is to run with true periodic boundary conditions and check the displacements on the edges.