Isotropic Material Failure Surface
Introduction
This damage initiation law predicts that failure initiates when maximum principal stress exceeds tensile strength of the material or when maximum shear stress exceeds shear strength of the material. It can also model pressure-dependent initiation stresses. Because it deals with principal stresses and tensile failure is the same regardless of direction, this law is only appropriate for isotropic materials such as an IsoSoftening material.
Failure Surface
Although some damage mechanics papers allow various initiation criteria to be be paired with various damage evolution methods, that suggestion is wrong. Instead, the initiation law must be identical to the postulated traction failure surface with the initiation stress equal to the undamaged strength in the damage mechanics softening laws. This initiation law thus uses the chosen failure surface with the initiation normal stress, [math]\displaystyle{ \sigma_c }[/math] equal to the undamage tensile strength and the initiation shear stress, [math]\displaystyle{ \tau_c }[/math], equal to undamaged shear strength (both of which are entered as parameters in this law).
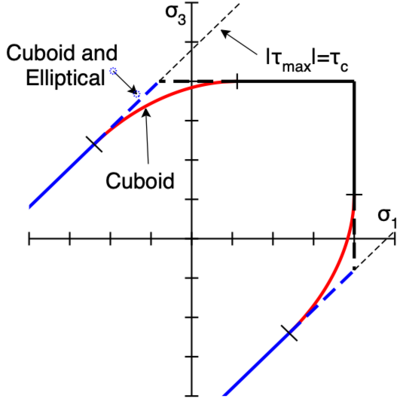
A challenge when detecting initiation, however, is that crack normal is not yet defined and therefore one cannot find tractions on the crack plane. In brief, damage initiation must determine when traction along any normal in 3D space reaches a failure surface. This calculation is done in principal stress space and finds critical stress by Mohr's circle calculations (more details are given in Ref. [1]). The plot on the right shows the resulting initiation failure surfaces in a plot of minimum vs. maximum principle stresses. Stress states that reach these plots cause initiation of damage. The crack normal is given by the normal at the point where stress state reaches the surface. This normal is with respect to principal stress directions and that is rotated into global axes to get normal to the initiated crack surface. In this plot the 45 degree lists are when maximum shear stress ([math]\displaystyle{ \tau_{max}=(\sigma_1-\sigma_3)/2 }[/math]) is equal to shear strength.
IsoSoftening materials can choose ovoid, cuboid, or elliptical failure surfaces using its tractionFailureSurface property. The solid line in the plot is for ovoid surfaces. The dashed lines are for both cuboid and elliptical failure surfaces. For ovoid surfaces, the normal varies smoothly from 0 to 45 degrees as failure transitions from tensile to shear failure. For cuboid and elliptical surfaces, cracks are either at 0 degrees or 45 degrees. IsoDamageMechanics materials use the cuboid surface, but only need that surface when using its mixed-mode metric. This material handles initiation internally rather than selecting an initiation law.
Pressure Dependent Shear Strength
Although generalized damage mechanics[1] provides a method to allow the failure surface to depend on any external variable, the only external dependence currently modeled is to allow shear strength to depend on pressure. This pressure dependence is only implement for IsoSoftening materials and IsoPlasticSoftening materials.
Model 0: shear strength is independent of pressure
Model 1: shear strength is linear in pressure:
[math]\displaystyle{ \tau = \tau_c\left(1 + {P\over \tau_h}\right) }[/math]
where [math]\displaystyle{ \tau_h }[/math] is hydrostatic tension that causess shear strength to reach zero under hydrostatic tension when [math]\displaystyle{ P=-\tau_h }[/math]. Note with out pressure dependence, a material never failures by shear strength in hydrostatic stress states. Furthermore, [math]\displaystyle{ \tau_h }[/math] must be higher the normal strength [math]\displaystyle{ \sigma_c }[/math].
Model 2: shear strength is step linear. The shear strength below [math]\displaystyle{ P_1 }[/math] is equal to basic shear strength, [math]\displaystyle{ \tau_c }[/math], but for [math]\displaystyle{ P\gt P_1 }[/math], it increases linearly to [math]\displaystyle{ \tau_{max} }[/math] at [math]\displaystyle{ P_2 }[/math]. Above [math]\displaystyle{ P_2 }[/math], the shear strength is constant and equal to [math]\displaystyle{ \tau_{max} }[/math]. For [math]\displaystyle{ P\gt P_1 }[/math], the shear strength is
[math]\displaystyle{ \tau = \tau_c + {\tau_{max}-\tau_c \over P_2-P_1}\bigl(\min(P,P_2)-P_1\bigr) }[/math]
Model 3: shear stength is exponential with an asymptote. The shear strength below [math]\displaystyle{ P_1 }[/math] is equal to basic shear strength, [math]\displaystyle{ \tau_c }[/math], but for [math]\displaystyle{ P\gt P_1 }[/math], it increases exponentially and asymptotically to [math]\displaystyle{ \tau_{max} }[/math]. For [math]\displaystyle{ P\gt P_1 }[/math], the shear strength is
[math]\displaystyle{ \tau = \tau_c + (\tau_{max}-\tau_c)\left(1-\exp\left(-{\ln 2 (P-P_1)\over P_2}\right)\right) }[/math]
Note that [math]\displaystyle{ P_2 }[/math] (which must be > 0) is the pressure increment above [math]\displaystyle{ P_1 }[/math] required for the shear strength to be half way between [math]\displaystyle{ \tau_c }[/math] and [math]\displaystyle{ \tau_{max} }[/math].
Model 4: shear stength is sigmoidal exponential. The shear strength evolves from [math]\displaystyle{ \tau_c }[/math] to [math]\displaystyle{ \tau_{max} }[/math] using a sigmoidal shape that is half way to [math]\displaystyle{ \tau_{max} }[/math] at [math]\displaystyle{ P_1 }[/math] and 1/3 or 2/3 of the way there as [math]\displaystyle{ P_1\mp P_2 }[/math]. For all [math]\displaystyle{ P }[/math], the shear strength is
[math]\displaystyle{ \tau = \tau_c + {(\tau_{max}-\tau_c)\over 1+\exp\left(-{\ln 2 (P-P_1)\over P_1}\right)} }[/math]
Some pressure-dependent examples suggest this model is the most stable.
A complication when using pressure dependence properties is the stability of damage mechanics depends on the strength properties. To allow this calculation at the beginning of the calculations the simulations should set maxPressure property to the maximum pressure expected during the simulation.
Damage Law Properties
The following table lists the input properties for maximum principal stress failure surface:
| Property | Description | Units | Default |
|---|---|---|---|
| sigmac | Critical tensile stress for failure | pressure units | infinite |
| tauc | Critical shear stress for failure | pressure units | infinite |
| PressureModel | Pick a model (0 to 4) to model pressure dependent shear strength | none | 0 |
| tauh | Hydrostatic tension that causes shear strength to drop to zero for pressure model 1 or maximum shear strength for pressure models 2, 3, and 4 | pressure units | infinite |
| P1 P2 |
Break points for shear strength in pressure models 2, 3, and 4 | pressure units | 0 for P1 |
| maxPressure | The maximum pressure expected in a simulations. It is used to verify damage mechanics stability at the start of the simulation. | pressure units | 0 |