Difference between revisions of "Isotropic Material Failure Surface"
| Line 8: | Line 8: | ||
[[File:FailureSurfacePlots.png|400px|right]] | [[File:FailureSurfacePlots.png|400px|right]] | ||
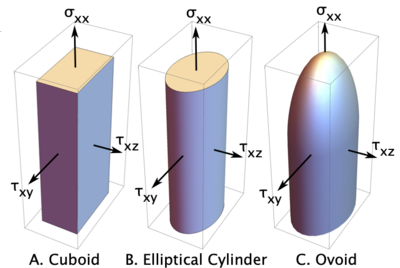
Three possible failure stress failure surfaces are shown in the figure. Which surface to use for initiation is determined by the <tt>tractionFailureSurface</tt> property of the parent [[Isotropic Softening Material|isotropic softening material]]. The calculations for | Three possible failure stress failure surfaces are shown in the figure. The surface along each axis gives the current strength by that stress. The current strength may depended on external variables such as pressure, strain rate in more. During damage evolution, the current strength will also depend on current damage state. Which failure surface to use for initiation and subseqent damage evolution is determined by the <tt>tractionFailureSurface</tt> property of the parent [[Isotropic Softening Material|isotropic softening material]]. The calculations for current strength transpose these surfaces to principle stress space and find critical stress by Mohr's circle calculations. The details are given in Ref. <ref name="dmGen"/>. | ||
=== Pressure Dependent Shear Strength === | |||
Although generalized damage mechanics<ref name="dmGen"/> provides a method to allow the failure surface to depend on any external variable, the only external dependence currently modeled is to allow shear strength to depend on pressure. | |||
== Damage Law Properties == | == Damage Law Properties == | ||
Revision as of 14:28, 31 January 2023
Introduction
This damage initiation law predicts that failure initiates when maximum principal stress exceeds tensile strength of the material or when maximum shear stress exceeds shear strength of the material. It can also model pressure-dependent initiation stresses. Because it deals with principal stresses and tensile failure is the same regardless of direction, this law is only appropriate for isotropic materials such as an IsoSoftening material.
Failure Surface
Three possible failure stress failure surfaces are shown in the figure. The surface along each axis gives the current strength by that stress. The current strength may depended on external variables such as pressure, strain rate in more. During damage evolution, the current strength will also depend on current damage state. Which failure surface to use for initiation and subseqent damage evolution is determined by the tractionFailureSurface property of the parent isotropic softening material. The calculations for current strength transpose these surfaces to principle stress space and find critical stress by Mohr's circle calculations. The details are given in Ref. [1].
Pressure Dependent Shear Strength
Although generalized damage mechanics[1] provides a method to allow the failure surface to depend on any external variable, the only external dependence currently modeled is to allow shear strength to depend on pressure.
Damage Law Properties
The following table lists the input properties for maximum principal stress failure surface:
| Property | Description | Units | Default |
|---|---|---|---|
| sigmac | Critical tensile stress for failure | pressure units | infinite |
| tauc | Critical shear stress for failure | pressure units | infinite |