Isotropic Softening Material

Constitutive Law

This MPM Material is an isotropic, elastic material, but once it fails, it develops anisotropic damage. The constitutive law for this material is

      [math]\displaystyle{ \mathbf{\sigma} = (\mathbf{I} - \mathbf{D}) \mathbf{C}( \mathbf{\varepsilon}- \mathbf{\varepsilon}_{res}) }[/math]

where C is stiffness tensor for the underlying isotropic material and D is an anisotropic 4^th rank damage tensor appropriate for damage in isotropic materials, and [math]\displaystyle{ \mathbf{\varepsilon}_{res} }[/math] is any residual strain (such as thermal or solvent induced strains).

An appropriate damage tensor was first proposed by Chaboche, and was implemented in mpm using this material typel for complete modeling of anisotropy caused by 3D damage evolution. This fourth rank tensor depends on three damage variables, which can be shown to relate to one tensile and two shear damage processes related to a crack plane. These three damage variables can be related to mode I and lumped mode II/III fracture mechanics failure modes.

Damage Initiation

Damage initiation is controlled by attaching a damage initiation law to the material. These laws define a failure envelop. Once the response reaches the envelop, the damage process is initiated and the normal to the envelop defines the normal to the crack plane modeled by this damage mechanics material. The normal is needed to find the anisotropic D tensor (which involves rotating analysis into the crack axis system where the x axis is aligned with the crack normal.

Predamage on any particle at the start of a simulation can be set using initial particle damage using particle boundary conditions.

Damage Evolution

Damage evolution is determined by softening laws to predict degradation of normal and shear tractions across the crack plane. You need to attach two softening laws to this material. These two laws handle tensile and shear damage and the areas under the laws correspond to fracture toughnesses G_Ic and lumped G_IIc/G_IIIc for the material.

In brief, this material models crack initiation and propagation through damage mechanics. The softening law's properties tie the damage mechanics to toughness properties for the material. The scheme can handle interacting cracks (which become interacting damage zones) and 3D cracks. MPM modeling using this material is described in a recent paper. A second paper shows that damage mechanics and fracture mechanics can give identical results provided damage parameters are appropriately chosen.

Damage Generalizations

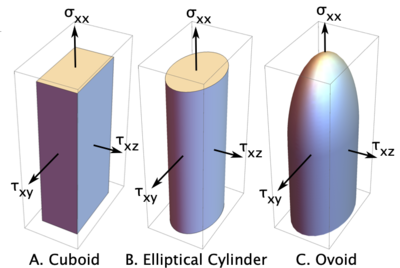
A third paper generalizes anisotropic damage mechanics including a method to couple damage parameters for more realistic modeling and to model pressure dependent failure properties. This coupling is based on choice of a traction failure surface and the three options are pictured on the right. These surfaces show failure surface in terms of current normal and shear tractions on the crack surface (they are for crack opening or tension on the crack surface; the changes for compression are described below). The response for each are as follows:

• Cuboid (0): This option provides uncoupled damage mechanics. Each direction evolves damage independently. If any direction exceeds the surface, it returns to an evolved surface in a direction normal to the surface. Although this approach is common in damage and cohesive zone modeling, the lack of coiupling means that damage in one direction does not influence loading in other directions. Imagine loading a material in tension such that it causes much damage but does not cause failure. If that material was unloaded and then reloaded in shear, the use of uncoupled damage parameters means it would act like a virgin material with no damage. Because this response is likely unrealistic, the other two surface add coupling options.
• Elliptical Cylinder (1): This option couples shear directions only. If traction exceeds the surface, it returns normal to the cylinder to an evolved state, but that state will evolve damage in both shear directions. The tensile damage is still decoupled and occurs when traction exceeds top of the cylinder. The next surface couples in tension as well.
• Ovoid (2): This option couples all directions. If the crack surface traction exceeds this surface, it returns to an evolved surface by following a path in the direction of the origin. By this approach, the tractions in all directions simultaneously reach zero at failure. In effect, damage variables are coupled such that d_n = d_xy = d_xz = d, but the damage crack opening variables (δ_n, δ_xy, and δ_xz parameters) will remain different.
• Coupled Cuboid (3): This option uses the cuboid failure surface but combines that with the full coupling of the ovoid surface. In brief, if an traction direction exceeds the cuboid surface, the damage evolves by returning to a new cuboid surface by a path to the origin rather than by a path normal to the cuboid surface. This approach keeps the damage parameters coupled (i.e., d_n = d_xy = d_xz = d) and guarantees all components of traction simultaneously reach zero at failure.

This picture does not show behavior when crack surfaces are in contact. The cuboid and elliptical cylindrical surface extend their shapes to the compression half plane with no limit (i.e., no normal direction failure in compression). The ovoid surface uses an infinite elliptical cylinder in compression but damage evolution follows a path to the origin rather then normal to the surface. In other words, shear damage that occurs in compression evolves tensile damage parameters as well to keep all directions coupled.

These failure surfaces are selected with the tractionFailureSurface material property and ovoid is currently the default failure surface.

Pressure Dependent Shear Strength

This material can model pressure dependent shear strength using the pressure models define in the isotropic initiation law. The calculations done during damage evolution, however, are done in the constitutive law calculations for this material. The calculations require an iterative process to keep the pressure increment consistent with pressure-dependent changes in strength and damage evolution. The numerics of this loop can be adjusted with the PDTol and PDPasses material properties, but the provided default values seem to work well.

White Noise Statistical Variations

Damage mechanics is often more realistic when the strength and/or toughness of the material points have statistical variations. The recommended way to model these statistical variations is to use Gaussian random fields, but that takes more work. A simple option in this material is to just randomly assigned relative strengths and/or toughness to material points at the start of the simulation. This method is a special case of a Gaussian random field with the spatial correlation function being a step function equal to the particle radius. In other words, this method will depend on mesh size and cannot vary spatial effects to match real materials. Nevertheless, simulations with damage mechanics materials are often improved by adding some white noise statistical variations. This option is especially helpful in problems where boundary conditions cause premature damage initiation.

Statistical variations can use a normal distribution or a Weibull distribution. The chosen distribution is used to assign relative strength or toughness for each material point. The values are relative to strength in the damage initiation law or toughness in the softening law for this material. The relative values can apply to strength alone, toughness alone, or to both strength and toughness. The one that are varied are set using the statDistributionMode property. The statistical values can be visualized by viewing history 12 or 13 (which remain constant throughout the simulation).

Normal Distribution

When using a normal distribution, the cumulative distribution for probability, [math]\displaystyle{ p }[/math], that a relative value is less then [math]\displaystyle{ r }[/math] is

     [math]\displaystyle{ p = \frac{1}{2}\left[1 + {\rm erf}\left( \frac{r-1}{C_v\sqrt{2}}\right)\right] }[/math]

where [math]\displaystyle{ C_v }[/math] is coefficient of variation of the distribution (entered with coefVariation parameter). When using this distribution, a simulation starts by randomly picking [math]\displaystyle{ p }[/math] (over the interval 0.001 to 0.999 that corresponds to ±3.09 standard deviations) and then numerical solving for [math]\displaystyle{ r }[/math]. This calculation is done for each particle. Note that if entered coefVariation is greater than 32.4%, the range of relative strengths will include negative numbers. To avoid zero or negative values, the minimum relative value allowed is 0.05. To avoid this truncation giving poorly-scaled results, problems that need very high coefficient of variation should use the Weibull distribution described in the next section.

Weibull Distribution

When using a two-parameter Weibull distribution, the cumulative distribution for probability, [math]\displaystyle{ p }[/math], that a relative value is less then [math]\displaystyle{ r }[/math] is

     [math]\displaystyle{ p = 1 - \exp\left(-\frac{V_p}{V_0}\left(r\Gamma\left(1+\frac{1}{\alpha}\right)\right)^\alpha\right) }[/math]

where [math]\displaystyle{ V_0 }[/math] (entered using wV0) and [math]\displaystyle{ \alpha }[/math] (entered wShape) are Weibull reference volume and shape parameters. For simulations where particles volumes, [math]\displaystyle{ V_p }[/math], may differ, this distribution introduces some size effects into the statistical calculations. When using this distribution, [math]\displaystyle{ r }[/math] is interpreted as value relative to the value at the reference volume [math]\displaystyle{ V_0 }[/math].

The mean and coefficient of variation for the relative value distribution are:

     [math]\displaystyle{ \langle r\rangle = \left(\frac{V_0}{V_p}\right)^{1/\alpha} \quad {\rm and} \quad C_v=\frac{\sqrt{\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma\left(1+\frac{1}{\alpha}\right)^2}}{\Gamma\left(1+\frac{1}{\alpha}\right)} }[/math]

When using this distribution, a simulation starts by randomly picking [math]\displaystyle{ p }[/math] (over the interval 0.001 to 0.999) and then solving for [math]\displaystyle{ r }[/math].

     [math]\displaystyle{ r = \frac{1}{\Gamma\left(1+\frac{1}{\alpha}\right)}\left[-\frac{V_0}{V_p}\ln(1-p)\right]^{1/\alpha} }[/math]

This calculation is done for each particle. To avoid zero relative values, the minimum relative value allowed is 0.05.

Unlike a normal distribution, a Weibull distribution is only defined for positive [math]\displaystyle{ r }[/math], which means it can be used for high-coefficient-of-variation distributions without truncating the curve. Because a normal distribution starts truncating when CV is greater than 32.4%, switching to a Weibull distribution might work better. Some high coefficients of variation can be modeled with the following Weibull shape parameters:

Shape Parameter	Coefficient of Variation (%)
1	100
2	52.2723
3	36.3447
4	28.0544

Although higher shape parameters are allowed, that option does not add anything to stochastic modeling of failure. If one plots the normal distribution and the Weibull distribution cumulative distribution functions ([math]\displaystyle{ p }[/math] defined above), the curves are essentially identical for coefficient of variation less than 30%. The only time a Weibull distribution might benefit simulations is when modeling materials with a very high coefficient of variation and that could be done by using a Weibull distribution with a low shape parameter.

Using Gaussian Random Fields

A more realistic method to a account for variations in strength or toughness is to use a Gaussian random field. In brief, a Gaussian random field is a realization of a property that follows a normal distribution but also has a spatial correlation function. Such a field is more realistic because "strong" areas are likely to be near other "strong" areas and similarly for "weak" areas. The above white noise methods may have a very "strong" particle next to a "weak" one. Another advantage of Gaussian random fields is that the spatial correlation function can use actual dimensions such that the statistical model will be less dependent on problem resolution.

The current code does not have a feature to generate Gaussian random fields. Instead, this method is done by generating Gaussian random fields in other software with dimensions matching the MPM simulation. This fields can be saved as images or text files that can input to a PropertyRamp Custom Task to set relative strength and/or relative toughness. Generating results with Gaussian random fields typically requires running the simulations multiple times with each one using a different realization of a Gaussian random field.

Material Properties

When the material is undamaged, it response is identical to properties entered for the underlying isotropic material. Once those are specified, you have to attach one damage initiation law and two softening laws to define how the material responds after initiation of damage.

Property	Description	Units	Default
(Isotropic Properties)	Enter all properties needed to define the underlying isotropic material response	varies	varies
Initiation	Attach damage initiation law by name or ID that is compatible with isotropic materials. Once attached, enter all required material properties for that law.	none	IsoFailure
SofteningI	Attach a softening law (by name or ID) for propagation of tensile damage. Once attached, enter all required properties for that law by prefacing each property with "I-".	none	Linear
SofteningII	Attach a softening law (by name or ID) for propagation of shear damage. Once attached, enter all required properties for that law by prefacing each property with "II-".	none	Linear
tractionFailureSurface	Selects traction failure surface and coupling methods as disucssed above above. The options are 0 = cuboid, 1 = cylindrical, 2 = ovoid. 3 = coupled cuboid. For cuboid, the three damage parameters evolve independently. For cylindrical, the two shear parameters are coupled but tension and shear are independent. For ovoid, all three damage parameters are coupled. Coupled cuboid couples the three damage parameters in cuboid to one damage parameter. For backward compatibility, old files with the deprecated shearFailureSurface property are accepted and its rectangular and elliptical options are converted to cuboid (which is identical to prior rectangular option) and the new elliptical cylinder (which corrects prior elliptical option) methods.	none	0
coefVariation	This property sets a coefficient of variation when assigning relative failure properties using a normal distribution. The property that is affected is determined by the statsDistributionMode parameter. A better approach to stochastic modeling would use Gaussian random fields with spatial correlation.	none	0
wShape wV0	These two properties set shape and reference volume when assigning relative failure properties using a Weibull distribution. The property that is affected is determined by the statsDistributionMode parameter. A better approach to stochastic modeling would use Gaussian random fields with spatial correlation.	none	none
statDistributionMode	The options are 1 = vary only strength, 2 = vary only toughness, and 3 = vary strength and toughness. Note that strength, toughness, and critical crack opening displacement (COD) are interrelated. Option 1 means COD will increase to keep toughness constant; 2 means COD will decrease to keep strength constant; 3 means COD will remain constant.	none	1
coeff	coefficient of friction for post-decohesion contact (default is 0 or frictionless) (experimental implementation in development in OSParticulas only)	none	0
PDTol	Tolerance to detect converge in loop to model pressure dependen shear strength.	none	1e-9
PDPasses	The maximum number of iterations allowed without convergence in the loop to model pressure dependen shear strength.	none	10
(other)	Properties common to all materials	varies	varies

Note that entering coefVariation means to use a normal distribution while entering either wShape or wV0 means to use a Weibull distribution. If both are entered, that last one entered will detemine which distribution is used.

Deprecated Material Properties

The following softening materials are no longer valid for the reasons given below.

Property	Description	Units	Default
shearFailureSurface	Select failure surface assumed when modeling shear damage in 3D calculations. Use 1 for an elliptical failure criterion based on current degraded shear strengths. Use 0 for a rectangular failure surface that encloses the elliptical failure criterion. The elliptical surface is preferred, but rectangular is more efficient.	none	1
	Reason: The two methods give similar results and some new theory showed that the elliptical coupling method did not couple shear damage properly. This property was deprecated January 6, 2020.
coefVariationMode	Simply a name change and it is identical to the new statDistibutionMode	none	1
	Reason: The name was changed when Weibull distribution was added because it now refers to different properties and not just the coefficient of variation.

History Variables

This material stores several history variables that track the extent of the damage and orientation of the damage plane:

1. The current damage state with the following possible values:
   • 0.1: indicates undamaged material. Note that undamaged value of 0.1 is to facilitate mapping of damage state to a grid such that undamaged regions can be distinguished by thresholding from empty regions (with zero damage).
   • 0.9, 1.0, or 1.1: indicates damage has initiated but particle has not yet failed. The three values are
     • 0.9: damage initiated by tensile failure
     • 1.0: damage initiation by both in-plane principle stresses exceeding tensile strength
     • 1.1: damage initiated by shear failure
   • Between 2 and 3: particle has failure by decohesion. After failure, the fraction energy dissipated by mode I damage is G_I/G_total = h[1]-2 or 2 is pure mode II failure, 3 is pure mode I failure, and anything between is mixed-mode failure.
2. δ_n or the maximum normal cracking strain.
3. δ_xy or the maximum x-y shear cracking strain.
4. This variable has two options:
   • For 3D when using cuboid surface: δ_xz or the maximum x-z cracking strain.
   • For all other cases: G_I or cumulative mode I dissipated energy.
5. d_n or damage variable for normal loading. It varies from 0 to 1 where 1 is complete damage or failure.
6. d_xy or damage variable for x-y shear loading. It varies from 0 to 1 where 1 is complete damage or failure.
7. This variable has two options:
   • For 3D when using cuboid surface: d_xz or damage variable for x-z shear loading (from 0 to 1 where 1 is complete damage or failure).
   • For all other cases: G_II or cumulative mode II dissipated energy.
8. For 2D it is cos(θ), but for 3D it is Euler angle α.
9. For 2D it is sin(θ), but for 3D it is Euler angle β.
10. For 3D it is Euler angle γ. In 2D has total dissipated energy by damage mechanics (in energy units)
11. A_c/V_p where A_c is crack area within the particle and V_p is particle volume.
12. Relative strength derived at the start by coefVariation and coefVariationMode properties.
13. Relative toughness derived at the start by coefVariation and coefVariationMode properties.

Variables 8-10 define the normal to the damage crack plane. For 2D, θ is the counter clockwise angle from the x axis to the crack normal. For 3D, (α, β, γ) are the three Euler angles for the normal direction using a Z-Y-Z rotation scheme. You can use the damagenormal archiving option to save enough information for plotting the normal. Although damaged normal is a unit vector, it is archived with magnitude equal to A_c/V_p (which gets another history variable archived and the value is used for some visualization options).

This material also tracks the cracking strain which can be saved by using the plasticstrain archiving option. The strain is archived in the global axis system. If you also archive the damagenormal, you will be able to plot a vector along the crack-opening displacement vector.

Examples

Material "isosoft","Isotropic Softening Material",50
  E 1000
  nu .33
  a 60
  rho 1
  largeRotation 1
  Initiation MaxPrinciple
  sigmac 30
  tauc 20
  SofteningI Linear
  I-Gc 10000
  SofteningII Linear
  II-Gc 10000
Done