Imperfect Interfaces

Both NairnMPM and NairnFEA can model imperfect interfaces between phases in composite structures.

Imperfect Interface Theory

Modeling interfaces, which are often finite-thickness interphases, in composite materials is difficult. In numerical modeling, it would seemingly be straight-forward to discretize interphase zones and thereby explicitly model all effects. This approach has two problems. First, interphase zones may be much smaller than the bulk materials. Resolving both bulk materials and a thin interphase would require a highly refined model, which may exceed computational capacity. Second, interphase properties may be unknown and/or may vary within a transition zone from one material to another. Alternative methods for interphase modeling are needed to overcome these challenges. This need is especially important in nanocomposites because the amount of interphase per unit volume of reinforcement greatly exceeds the amount of interphase in composites with micron or larger reinforcement phases. As a consequence, interphases are expected to play a larger role, good or bad, in nanocomposite properties.

One way to model interphases is to abandon attempts for explicit modeling and instead replace 3D interphases with 2D interfaces The interphase effects are reduced to modeling the response of 2D interfaces due to tractions normal and tangential to the interfacial surface, which can be modeled by interface traction laws. Elimination of 3D interphases removes the resolution problem. The use of interface traction laws also replaces numerous unknown and potentially unmeasurable interphase properties with a much smaller number of interface parameters. If interface traction laws can be determined, one can potentially model interphase effects well. Examples of using this for analytical modeling of interface effects in composite materials are in Hashin (1991) and Nairn and Liu (1997). Implementation of imperfect interfaces in FEA and in MPM is described in Nairn (2007). An alternative method for modeling imperfect interfaces in MPM using multimaterial MPM is described in Nairn (2013).

Imperfect Interface Traction Laws

To model 3D interphase effects using imperfect interfaces, the 2D interface is allowed to develop displacement discontinuities. For an isotropic interphase, it suffices to resolve interfacial traction into normal and tangential tractions (T_n and T_t) and assume they are functions of normal and tangential displacement discontinuities ([u_n] and [u_n]) at the interface:

      [math]\displaystyle{ T_n = f_n([u_n]) \qquad {\rm and } \qquad T_t = f_t([u_t]) }[/math]

Interfaces in composite materials may develop potential energy that is needed for effective property analysis. For an elastic interface, interfacial potential energy is:

      [math]\displaystyle{ \phi_i = \int_{S_i}\left(\int \vec T\cdot[d\vec u]\right) dS }[/math]

where S_i is interfacial area.

The simplest assumption for traction laws is that they are linear and elastic. The tractions become:

      [math]\displaystyle{ T_n = D_n[u_n] \qquad {\rm and } \qquad T_t = D_t[u_t] }[/math]

and interfacial energy becomes

      [math]\displaystyle{ \phi_i = {1\over2} \int_{S_i} \left( D_n[u_n]^2 + D_t[u_t]^2\right) dS }[/math]

Notice that all 3D interphase properties have been reduced to just two interface parameters, D_n and D_t. These interface stiffnesses range from zero, for a debonded interface with no tractions, to infinity, for a perfect interface with no displacement discontinuity.

Imperfect Interfaces in MPM

In NairnMPM, imperfect interface can be modeled using either explicit cracks or using multimaterial mode MPM. The use of cracks works well for interfaces within a single material. The use of multimaterial mode works well for material-material interfaces in composites.

Imperfect Interfaces on Explicit Cracks

Explicit cracks in NairnMPM can model imperfect interface mechanics on crack surfaces. In this mode, the cracks are actually internal interfaces rather than cracks. To set up calculations where cracks are interfaces in scripted input files, use the command

ImperfectInterface (Dt),(Dntens),(Dncomp)

In XML files, cracks as imperfect interfaces are set up with a modified <Friction> command within the <Cracks> element in the <MPMHeader>:

<Friction Dt="(Dt)" Dn="(Dntens)" Dnc="(Dncomp)">11</Friction>

The parameters are described below.

The above commands set the default imperfect interface parameters for crack surfaces. When a simulation only has only one crack, this setting is enough. For simulations with more than one crack, you can set different imperfect interface parameters for each crack, or convert some cracks to frictional sliding, by using settings available when defining the cracks.

Imperfect Interfaces in Multimaterial MPM

Multimaterial mode MPM can implement imperfect interface mechanics at all nodes seeing more than one material. This type of analysis is best suited to modeling interface effects in complex 2D or 3D composite materials. To set up interface calculations in scripted MPM files, use the command

ImperfectInterfaceMM (Dt),(Dntens),<(Dncomp)>

In XML files, imperfect interfaces are set up with a modified <Friction> command within the <MultimaterialMode> element:

<Friction Dt="(Dt)" Dn="(Dntens)" Dnc="(Dncomp)">11</Friction>

where

• (Dt) is the imperfect interface parameter in the tangential direction (in MPa/mm)
• (Dntens),(Dncomp) are the imperfect interface parameters for the normal direction (in MPa/mm). The use of two parameters allows modeling of non-linear interfaces that have different stiffness in the tensile and compressive directions. In other words, (Dntens) is the interface parameter when the surface are separated and therefore in tension. (Dncomp) is the interface parameter with the surfaces are in contact and therefore in compression. If only (Dntens) is specified (which can also use a Dnt attribute), the interface will be linear and have the same stiffness in tension and compression.

In XML files, the value of of the <Friction> element should be greater than 10 as a flag to indicate material contact is modeled as an interface rather than frictional contact.

In theory, the interface becomes perfect in either direction as the interface parameters approach infinity, but high values for stiffness make the problem numerically unstable (unless very small time steps are used). To make the interface perfect in any direction, set the stiffness to -1, instead of using a high stiffness. A common situation is to model the interface as perfect in compression but imperfect in tension. Such an interface can be created by setting (Dntens) to a stiffness value and (Dncomp)=-1.

The above commands set the default imperfect interface parameters for contact between any two materials. When a simulation only has two materials connected by an interface, this setting is enough. For simulations with more than two materials, you can set different interface parameters for each material pair, or even combine material pairs connected by an imperfect interfaces with those interacting by friction, by using a Friction or Interface material property for the secondly-defined material or each pair needing different contact mechanics.

Interfacial Energy

When an analysis has imperfect interfaces, you can track total interface energy using global archiving methods. In an elastic analysis, the total strain energy is the sum of the strain energy and the interface energy. You should use this total energy when calculating effective composite properties by energy methods,

Imperfect Interfaces in FEA

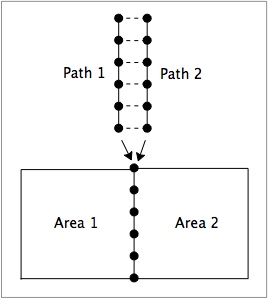
In NairnFEA, imperfect interfaces are modeling by inserting interface element. The procedure is as follows:

1. Define one or more imperfect interface materials and enter their interface parameters. Because NairnFEA is for linear elastic analysis only, the imperfect interface materials have to be linear elastic as well. In other words, the traction laws are linear with interface parameters D_n and D_t.
2. Define two different, but overlapping paths that have the some number and arrangement of nodes. In other words, define the paths with the same number of nodes, having the same ratio of element sizes, and using keypoints that are distinct but have matching coordinates.
3. Use the two paths in two areas for the two materials to be connected by an imperfect interface.
4. Use the two paths in an area command that uses interface elements that are compatible with the type of solid elements used in the areas in step 3 (i.e., linear interface with linear elements or a quadratic interface with quadratic elements).

Interfacial Stress and Strains

Because interface elements had zero thickness, they cannot define stresses and strains. They do, however, model displacement discontinuities and have tractions. The displacement discontinuities in calculations are found from the nodal displacements. The resulting interfacial tractions are output in the element stresses. The normal traction, T_n is output in σ_xx while the tangential traction, T_t, is output in τ_xy.

Interfacial Energy

When calculating effective composite properties using energy methods, it is necessary to include both strain energy and interfacial energy. When the FEA model has imperfect interfaces, their interfacial energy is output in element stain energy. The total energy from all elements is the sum of strain energy an interfacial energy.