Difference between revisions of "Isotropic Material Failure Surface"
| Line 8: | Line 8: | ||
[[File:MaxPrinciple.png|400px|right]] | [[File:MaxPrinciple.png|400px|right]] | ||
Although some damage mechanics papers allow various initiation criteria to be be paired with various damage evolution methods, that suggestion is wrong. Instead, the initiation law must be identical to the postulated traction failure surface with the initiation stress equal to the undamaged strength in the damage mechanics softening laws. This initiation law thus uses the [[ | Although some damage mechanics papers allow various initiation criteria to be be paired with various damage evolution methods, that suggestion is wrong. Instead, the initiation law must be identical to the postulated traction failure surface with the initiation stress equal to the undamaged strength in the damage mechanics softening laws. This initiation law thus uses the [[Isotropic Softening Material#Damage Evolution|chosen failure surface]] with the initiation normal stress, <math>\sigma_c</math> equal to the undamage tensile strength and the initiation shear stress, <math>\tau_c</math> equal to undamaged shear strength (both of which are entered as parameters in the law. | ||
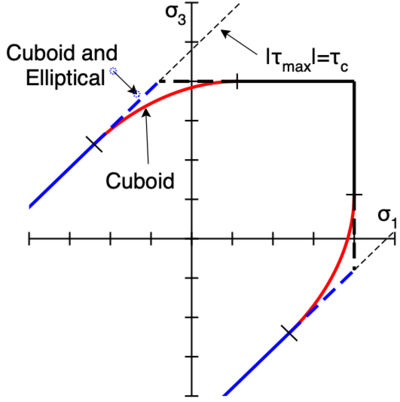
A challenge when detecting initiation, however, is that crack normal is not yet defined and therefore one cannot find tractions on the crack plane. In brief, damage initiation must determine when traction along any normal in 3D space reaches a failure surface. This calculation is done in principle stress space, The plot on the right shows the result initiation failure surfaces in a plot of maximum ''vs.'' minimum principle stresses. Stress states the reaches these plot causes initiation of damage. The crack normal is set equal to the normal to the point where stress state reaches the surface. This normal is respect to principal stress directions and that is rotated into global axes to get normal to the initiated crack surface. In this plot ''r'' is the maximum shear stress give by <math>(\sigma_1-\sigma_3)/2</math>. | |||
[[Isotropic Softening Material|IsoSoftening materials]] can choose cuboid, elliptical, or ovoid failure surfaces using the its <tt>tractionFailureSurface</tt>. The solid line in the plot is for cuboid surfaces. The dashed lines are for both cuboid and elliptical failure surface. Note that for cuboid and elliptical, cracks are either at 0 degrees of 45 degrees to the principal stress directions. For ovoid, the normal can vary smooth from 0 to 45 degrees and failure transitions for tensile to shear failure. For | |||
The initiation of failure in isotropic materials is found in principle stress space. The plot on the right shows the failure criterion in a 2D plot of minimum and maximum principle stresses. When the stress reaches any point on these surface, the damage is initiated. | |||
Three possible failure stress failure surfaces are shown in the figure. The surface along each axis gives the current strength by that stress. The current strength may depended on external variables such as pressure, strain rate in more. During damage evolution, the current strength will also depend on current damage state. Which failure surface to use for initiation and subseqent damage evolution is determined by the <tt>tractionFailureSurface</tt> property of the parent [[Isotropic Softening Material|isotropic softening material]]. The calculations for current strength transpose these surfaces to principle stress space and find critical stress by Mohr's circle calculations. The details are given in Ref. <ref name="dmGen"/>. | Three possible failure stress failure surfaces are shown in the figure. The surface along each axis gives the current strength by that stress. The current strength may depended on external variables such as pressure, strain rate in more. During damage evolution, the current strength will also depend on current damage state. Which failure surface to use for initiation and subseqent damage evolution is determined by the <tt>tractionFailureSurface</tt> property of the parent [[Isotropic Softening Material|isotropic softening material]]. The calculations for current strength transpose these surfaces to principle stress space and find critical stress by Mohr's circle calculations. The details are given in Ref. <ref name="dmGen"/>. | ||
Revision as of 16:42, 17 November 2023
Introduction
This damage initiation law predicts that failure initiates when maximum principal stress exceeds tensile strength of the material or when maximum shear stress exceeds shear strength of the material. It can also model pressure-dependent initiation stresses. Because it deals with principal stresses and tensile failure is the same regardless of direction, this law is only appropriate for isotropic materials such as an IsoSoftening material.
Failure Surface
Although some damage mechanics papers allow various initiation criteria to be be paired with various damage evolution methods, that suggestion is wrong. Instead, the initiation law must be identical to the postulated traction failure surface with the initiation stress equal to the undamaged strength in the damage mechanics softening laws. This initiation law thus uses the chosen failure surface with the initiation normal stress, [math]\displaystyle{ \sigma_c }[/math] equal to the undamage tensile strength and the initiation shear stress, [math]\displaystyle{ \tau_c }[/math] equal to undamaged shear strength (both of which are entered as parameters in the law.
A challenge when detecting initiation, however, is that crack normal is not yet defined and therefore one cannot find tractions on the crack plane. In brief, damage initiation must determine when traction along any normal in 3D space reaches a failure surface. This calculation is done in principle stress space, The plot on the right shows the result initiation failure surfaces in a plot of maximum vs. minimum principle stresses. Stress states the reaches these plot causes initiation of damage. The crack normal is set equal to the normal to the point where stress state reaches the surface. This normal is respect to principal stress directions and that is rotated into global axes to get normal to the initiated crack surface. In this plot r is the maximum shear stress give by [math]\displaystyle{ (\sigma_1-\sigma_3)/2 }[/math].
IsoSoftening materials can choose cuboid, elliptical, or ovoid failure surfaces using the its tractionFailureSurface. The solid line in the plot is for cuboid surfaces. The dashed lines are for both cuboid and elliptical failure surface. Note that for cuboid and elliptical, cracks are either at 0 degrees of 45 degrees to the principal stress directions. For ovoid, the normal can vary smooth from 0 to 45 degrees and failure transitions for tensile to shear failure. For
The initiation of failure in isotropic materials is found in principle stress space. The plot on the right shows the failure criterion in a 2D plot of minimum and maximum principle stresses. When the stress reaches any point on these surface, the damage is initiated.
Three possible failure stress failure surfaces are shown in the figure. The surface along each axis gives the current strength by that stress. The current strength may depended on external variables such as pressure, strain rate in more. During damage evolution, the current strength will also depend on current damage state. Which failure surface to use for initiation and subseqent damage evolution is determined by the tractionFailureSurface property of the parent isotropic softening material. The calculations for current strength transpose these surfaces to principle stress space and find critical stress by Mohr's circle calculations. The details are given in Ref. [1].
Pressure Dependent Shear Strength
Although generalized damage mechanics[1] provides a method to allow the failure surface to depend on any external variable, the only external dependence currently modeled is to allow shear strength to depend on pressure.
Model 0: shear strength is independent of pressure
Model 1: shear strength is linear in pressure:
[math]\displaystyle{ \tau = \tau_c\left(1 + {P\over \tau_h}\right) }[/math]
where [math]\displaystyle{ \tau_h }[/math] is hydrostatic tension that causess shear strength to reach zero under hydrostatic tension when [math]\displaystyle{ P=-\tau_h }[/math]. Note with out pressure dependence, a material never failures by shear strength in hydrostatic stress states. Furthermore, [math]\displaystyle{ \tau_h }[/math] must be higher the normal strength [math]\displaystyle{ \sigma_c }[/math].
Model 2: shear strength is step linear. The shear strength below [math]\displaystyle{ P_1 }[/math] is equal to basic shear strength, [math]\displaystyle{ \tau_c }[/math], but for [math]\displaystyle{ P\gt P_1 }[/math], it increases linearly to [math]\displaystyle{ \tau_{max} }[/math] at [math]\displaystyle{ P_2 }[/math]. Above [math]\displaystyle{ P_2 }[/math], the shear strength is constant and equal to [math]\displaystyle{ \tau_{max} }[/math]. For [math]\displaystyle{ P\gt P_1 }[/math], the shear strength is
[math]\displaystyle{ \tau = \tau_c + {\tau_{max}-\tau_c \over P_2-P_1}\bigl(\min(P,P_2)-P_1\bigr) }[/math]
Model 3: shear stength is exponential with an asymptote. The shear strength below [math]\displaystyle{ P_1 }[/math] is equal to basic shear strength, [math]\displaystyle{ \tau_c }[/math], but for [math]\displaystyle{ P\gt P_1 }[/math], it increases exponentially and asymptotically to [math]\displaystyle{ \tau_{max} }[/math]. For [math]\displaystyle{ P\gt P_1 }[/math], the shear strength is
[math]\displaystyle{ \tau = \tau_c + (\tau_{max}-\tau_c)\left(1-\exp\left(-{\ln 2 (P-P_1)\over P_2}\right)\right) }[/math]
Note that [math]\displaystyle{ P_2 }[/math] (which must be > 0) is the pressure increment above [math]\displaystyle{ P_1 }[/math] required for the shear strength to be half way between [math]\displaystyle{ \tau_c }[/math] and [math]\displaystyle{ \tau_{max} }[/math].
Model 4: shear stength is sigmoidal exponential. The shear strength evolves from [math]\displaystyle{ \tau_c }[/math] to [math]\displaystyle{ \tau_{max} }[/math] using a sigmoidal shape that is half way to [math]\displaystyle{ \tau_{max} }[/math] at [math]\displaystyle{ P_1 }[/math] and 1/3 or 2/3 of the way there as [math]\displaystyle{ P_1\mp P_2 }[/math]. For all [math]\displaystyle{ P }[/math], the shear strength is
[math]\displaystyle{ \tau = \tau_c + {(\tau_{max}-\tau_c)\over 1+\exp\left(-{\ln 2 (P-P_1)\over P_1}\right)} }[/math]
Some pressure-dependent examples suggest this model is the most stable.
A complication when using pressure dependence properties is the stability of damage mechanics depends on the strength properties. To allow this calculation at the beginning of the calculations the simulations should set maxPressure property to the maximum pressure expected during the simulation.
Damage Law Properties
The following table lists the input properties for maximum principal stress failure surface:
| Property | Description | Units | Default |
|---|---|---|---|
| sigmac | Critical tensile stress for failure | pressure units | infinite |
| tauc | Critical shear stress for failure | pressure units | infinite |
| PressureModel | Pick a model (0 to 4) to model pressure dependent shear strength | none | 0 |
| tauh | Hydrostatic tension that causes shear strength to drop to zero for pressure model 1 or maximum shear strength for pressure models 2, 3, and 4 | pressure units | infinite |
| P1 P2 |
Break points for shear strength in pressure models 2, 3, and 4 | pressure units | 0 for P1 |
| maxPressure | The maximum pressure expected in a simulations. It is used to verify damage mechanics stability at the start of the simulation. | pressure units | 0 |